题目内容
已知函数f(x)=|x2-2ax+b|(x∈R),则( )
| A、f(x)必是偶函数 |
| B、当f(0)=f(2)时,f(x)的图象关于直线x=1对称 |
| C、若a2-b≤0,则f(x)在区间[a,+∞)上是增函数 |
| D、f(x)有最大值|a2-b| |
考点:带绝对值的函数,二次函数的性质
专题:计算题,函数的性质及应用
分析:举反例a=b=1排除A;通过a=b=2,排除B;利用a2-b≤0时,函数y=x2-2ax+b与x轴没有交点,判断函数的单调性,求出单调区间,即可判断C的正误.举反例a=1,b=3排除D.
解答:
解:对于A,当a=b=1,f(x)=|x2-2x+1|不是偶函数,故排除A.
对于B,当a=2,b=2时,有f(x)=|x2-4x+2|,f(0)=f(2),但此函数关于x=1不对称.
对于C,a2-b≤0时,函数y=x2-2ax+b与x轴没有交点,f(x)=|x2-2ax+b|=x2-2ax+b,开口向上,对称轴为x=a,在区间[a,+∞)上单调递增.所以C正确.
对于D,当a=1,b=3 f(x)=|x2-2x+3|=x2-2x+3,函数的开口向上,函数没有最大值.所以D不正确.
故选:C.
对于B,当a=2,b=2时,有f(x)=|x2-4x+2|,f(0)=f(2),但此函数关于x=1不对称.
对于C,a2-b≤0时,函数y=x2-2ax+b与x轴没有交点,f(x)=|x2-2ax+b|=x2-2ax+b,开口向上,对称轴为x=a,在区间[a,+∞)上单调递增.所以C正确.
对于D,当a=1,b=3 f(x)=|x2-2x+3|=x2-2x+3,函数的开口向上,函数没有最大值.所以D不正确.
故选:C.
点评:本题主要考查了分段函数的性质:函数的奇偶性,函数的最值的求解,函数的对称性,函数的单调性,二次函数性质的应用.是一道综合性比较好的试题.

练习册系列答案
相关题目
三个数208,351,429的最大公约数是( )
| A、65 | B、91 | C、26 | D、13 |
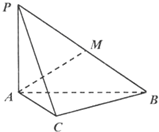 如图,三棱锥P-ABC中,∠ACB=90°,PA⊥底面ABC.
如图,三棱锥P-ABC中,∠ACB=90°,PA⊥底面ABC.