题目内容
长方体ABCD-A1B1C1D1中，AB=3，BC=3，AA1=4，则二面角D1-AB-D的余弦值是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：二面角的平面角及求法
专题：计算题,空间角
分析：由题意，∠D1AD是二面角D1-AB-D的平面角，即可求解．
解答：
解：由题意，∠D1AD是二面角D1-AB-D的平面角，
Rt△D1AD中，AD=3，DD1=4，∴AD1=5，
∴cos∠D1AD=
，
故选：A．
解：由题意，∠D1AD是二面角D1-AB-D的平面角，Rt△D1AD中，AD=3，DD1=4，∴AD1=5，
∴cos∠D1AD=
| 3 |
| 5 |
故选：A．
点评：本题考查二面角D1-AB-D的余弦值，确定二面角D1-AB-D的平面角是关键．
练习册系列答案
名校课堂系列答案
相关题目
下列四组中的函数f（x）与g（x），是同一函数的是（ ）
| A、f（x）=ln（1-x）+ln（1+x），g（x）=ln（1-x2） | ||||||
| B、f（x）=lgx2，g（x）=2lgx | ||||||
C、f（x）=
| ||||||
D、f（x）=
|
命题“?x0∈R，使得x03＜0”的否定为（ ）
| A、?x0∈R，使得x03≥0 |
| B、?x∈R，x3＜0 |
| C、?x∈R，使得x3≤0 |
| D、?x∈R，x3≥0 |
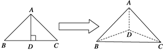如图，以等腰直角三角形斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，则下列四个结论中错误的是（ ）| A、BD⊥AC | ||
| B、△ABC是等边三角形 | ||
| C、平面ADC⊥平面ABC | ||
D、二面角A-BC-D的正切值为
|