题目内容
在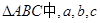 分别是角A、B、C的对边,
分别是角A、B、C的对边,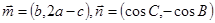 ,且
,且 .
.
(1).求角B的大小;
(2).求sin A+sin C的取值范围.
(1)B=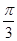 ;(2)
;(2) .
.
解析试题分析:(1)由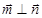 ,可得
,可得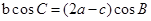 ,等式中边角混在了一起,需要进行边角的统一,根据正弦定理可得
,等式中边角混在了一起,需要进行边角的统一,根据正弦定理可得 ,进一步变形化简可得
,进一步变形化简可得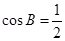 ,∴B
,∴B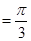 ;(2)由(1)可得
;(2)由(1)可得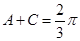 ,即
,即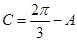 ,因此可以将sinA+sinC进行三角恒等变形转化为关于A的函数,即
,因此可以将sinA+sinC进行三角恒等变形转化为关于A的函数,即
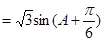 ,从而可以得到sinA+sinC取值范围是
,从而可以得到sinA+sinC取值范围是 .
.
(1) 由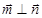 ,得
,得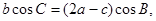
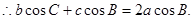
由正弦定理得: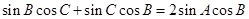 ,
,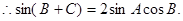 又
又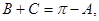
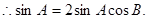
又 又
又 ;
;
∵ ,∴
,∴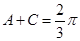 ,
,
∴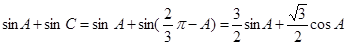
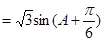 ,
,
∵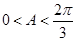 ,∴
,∴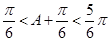 ,∴
,∴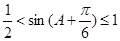 ,∴
,∴ .
.
故sin A+sin C的取值范围是 .
.
考点:1、平面向量垂直的坐标表示;2、三角恒等变形.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
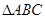 中,内角
中,内角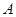 ,
, ,
,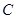 所对的边分别为
所对的边分别为 ,
,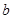 ,
,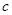 ,已知
,已知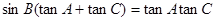 .
.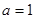 ,
,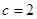 ,求
,求 .
. 中,
中, 分别为角
分别为角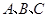 的对边,且满足
的对边,且满足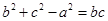 .
.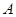 的值;
的值;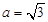 ,求bc最大值.
,求bc最大值. 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且
,且 ,
, ,
, .
. 与边
与边 在
在 方向上的投影.
方向上的投影.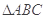 中,角
中,角 、
、 、
、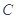 的对边分别为
的对边分别为 、
、 、
、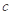 ,
, ,
, .
.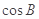 的值;(2) 设函数
的值;(2) 设函数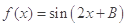 ,求
,求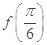 的值.
的值.

 ,向量
,向量
 .
. ,b+c=3,求b,c的长.
,b+c=3,求b,c的长. ,
, .
. 的值.
的值.