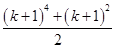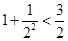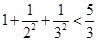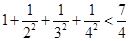题目内容
一个建设集团公司共有3n(n≥2,n∈N*)个施工队,编号分别为1,2,3,…3n.现有一项建设工程,因为工人数量和工作效率的差异,经测算:如果第i(1≤i≤3n)个施工队每天完成的工作量都相等,则它需要i天才能独立完成此项工程.
(1)求证第n个施工队用m(1≤m<n,m∈N*)天完成的工作量不可能大于第n+k(1≤k≤2n)个施工队用m+k天完成的工作量;
(2)如果该集团公司决定由编号为n+1,n+2,…,3n共2n个施工队共同完成,求证它们最多不超过两天即可完成此项工作.
(1)求证第n个施工队用m(1≤m<n,m∈N*)天完成的工作量不可能大于第n+k(1≤k≤2n)个施工队用m+k天完成的工作量;
(2)如果该集团公司决定由编号为n+1,n+2,…,3n共2n个施工队共同完成,求证它们最多不超过两天即可完成此项工作.
证明:(1)依题意,第i(1≤i≤3n)个施工队的工作效率为
…1分
故本题即是证明当1≤m<n,m∈N*且1≤k≤2n时,
<
…3分
∵
-
=
=
当1≤m<n,m∈N*且1≤k≤2n时,
<0显然成立,故命题得证.…6分
(2)要证明此命题,即是证明2(
+
+…+
)>1(n≥2,n∈N*),
也就是证明:
+
+…+
>
(n≥2,n∈N*).…9分
[法一]:利用数学归纳法:
(1)当n=2时,左边=
+
+
+
>
,不等式成立.
(2)假设当n=k(k≥2,k∈N*)时不等式成立.
即
+
+…+
>
.
则当n=k+1时,
+
+…+
+
+
+
=
+
+…+
+(
+
+
-
)>
+(3×
-
)=
.
所以当n=k+1时不等式也成立,
由(1),(2)知原不等式对一切n≥2,n∈N*均成立.…14分
[法二]利用放缩法:
∵n≥2,
∴
+
+…+
>
+
+…+
=
>
.
即
+
+…+
>
(n≥2,n∈N*).…14分.
| 1 |
| i |
故本题即是证明当1≤m<n,m∈N*且1≤k≤2n时,
| m |
| n |
| m+k |
| n+k |
∵
| m |
| n |
| m+k |
| n+k |
| mn+mk-mn-nk |
| n(n+k) |
| (m-n)k |
| n(n+k) |
当1≤m<n,m∈N*且1≤k≤2n时,
| (m-n)k |
| n(n+k) |
(2)要证明此命题,即是证明2(
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 3n |
也就是证明:
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 3n |
| 1 |
| 2 |
[法一]:利用数学归纳法:
(1)当n=2时,左边=
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 2 |
(2)假设当n=k(k≥2,k∈N*)时不等式成立.
即
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| 3k |
| 1 |
| 2 |
则当n=k+1时,
| 1 |
| ?k+1?+1 |
| 1 |
| ?k+1?+2 |
| 1 |
| 3k |
| 1 |
| 3k+1 |
| 1 |
| 3k+2 |
| 1 |
| 3k+3 |
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| 3k |
| 1 |
| 3k+1 |
| 1 |
| 3k+2 |
| 1 |
| 3k+3 |
| 1 |
| k+1 |
| 1 |
| 2 |
| 1 |
| 3k+3 |
| 1 |
| k+1 |
| 1 |
| 2 |
所以当n=k+1时不等式也成立,
由(1),(2)知原不等式对一切n≥2,n∈N*均成立.…14分
[法二]利用放缩法:
∵n≥2,
∴
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 3n |
| 1 |
| 3n |
| 1 |
| 3n |
| 1 |
| 3n |
| 2 |
| 3 |
| 1 |
| 2 |
即
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 3n |
| 1 |
| 2 |

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
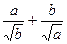 ≥
≥ .
. 成立.
成立.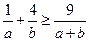 .
.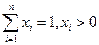 ,求证:
,求证: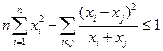 。
。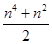 ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )