题目内容
17.已知函数g(x)=-$\frac{1}{x}$的图象关于点A(-$\frac{1}{2}$,$\frac{1}{2}$)的对称图象为函数y=f(x)的图象.(1)求y=f(x);
(2)用函数单调性的定义证明y=f(x)在(一1,+∞)上为单调递增函数.
分析 (1)设函数y=f(x)的图象上任一点(x,y),相应y=g(x)图象上一点为(m,n),运用中点坐标公式和代入法,即可得到所求f(x)的解析式;
(2)由单调性的定义,注意设自变量和作差、变形和定符号、下结论等步骤.
解答 解:(1)函数g(x)=-$\frac{1}{x}$的图象关于点A(-$\frac{1}{2}$,$\frac{1}{2}$)对称,
设函数y=f(x)的图象上任一点(x,y),相应y=g(x)图象上一点为(m,n),
可得x+m=-1,y+n=1,
即为m=-1-x,n=1-y,
代入g(x)=-$\frac{1}{x}$,可得1-y=-$\frac{1}{-1-x}$,
化为y=f(x)=$\frac{x}{x+1}$;
(2)证明:令x1>x2>-1,
则f(x1)-f(x2)=$\frac{{x}_{1}}{{x}_{1}+1}$-$\frac{{x}_{2}}{{x}_{2}+1}$=$\frac{{x}_{1}-{x}_{2}}{({x}_{1}+1)({x}_{2}+1)}$,
由x1>x2>-1,
可得x1-x2>0,x1+1>0,x2+1>0,
即有f(x1)-f(x2)>0,即f(x1)>f(x2),
可得y=f(x)在(-1,+∞)上为单调递增函数.
点评 本题考查函数的对称性和应用:求函数的解析式,考查单调性的证明,注意运用定义法,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
10.已知直线l过点P(2,-1),且与直线2x+y-l=0互相垂直,则直线l的方程为( )
| A. | x-2y=0 | B. | x-2y-4=0 | C. | 2x+y-3=0 | D. | 2x-y-5=0 |
12.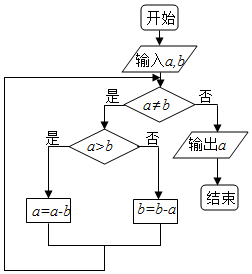 《九章算术》是我国古代数学名著,汇集古人智慧,其中的“更相减损术”更是有着深刻的应用.如图所示程序框图的算法思想即来源于此,若输入的a=2016,输出的a=21,则输入的b可能为( )
《九章算术》是我国古代数学名著,汇集古人智慧,其中的“更相减损术”更是有着深刻的应用.如图所示程序框图的算法思想即来源于此,若输入的a=2016,输出的a=21,则输入的b可能为( )
 《九章算术》是我国古代数学名著,汇集古人智慧,其中的“更相减损术”更是有着深刻的应用.如图所示程序框图的算法思想即来源于此,若输入的a=2016,输出的a=21,则输入的b可能为( )
《九章算术》是我国古代数学名著,汇集古人智慧,其中的“更相减损术”更是有着深刻的应用.如图所示程序框图的算法思想即来源于此,若输入的a=2016,输出的a=21,则输入的b可能为( )| A. | 288 | B. | 294 | C. | 378 | D. | 399 |
2. 某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.下面是年龄的分布表:
某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.下面是年龄的分布表:
(Ⅰ)求正整数a,b,N的值;
(Ⅱ)现要从年龄低于40岁的员工用分层抽样的方法抽取42人,则年龄在第1,2,3组得员工人数分别是多少?
(Ⅲ)为了估计该单位员工的阅读倾向,现对该单位所有员工中按性别比例抽查的40人是否喜欢阅读国学类书籍进行了调查,调查结果如下所示:(单位:人)
根据表中数据,我们能否有99%的把握认为该位员工是否喜欢阅读国学类书籍和性别有关系?
附:K2=$\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
 某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.下面是年龄的分布表:
某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.下面是年龄的分布表:| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) |
| 人数 | 28 | a | b |
(Ⅱ)现要从年龄低于40岁的员工用分层抽样的方法抽取42人,则年龄在第1,2,3组得员工人数分别是多少?
(Ⅲ)为了估计该单位员工的阅读倾向,现对该单位所有员工中按性别比例抽查的40人是否喜欢阅读国学类书籍进行了调查,调查结果如下所示:(单位:人)
| 喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
| 男 | 14 | 4 | 18 |
| 女 | 8 | 14 | 22 |
| 合计 | 22 | 18 | 40 |
附:K2=$\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |