题目内容
某货轮在A处看灯塔B在货轮的北偏东75°的方向上,距离为12
海里,在A处看灯塔C在货轮的北偏西30°的方向上,距离为8
海里,货轮由A处向正北航行到D处时,再看灯塔B在南偏东60°方向上,求:
(1)AD的距离;
(2)CD的距离.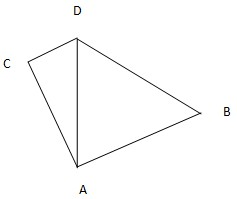
| 6 |
| 3 |
(1)AD的距离;
(2)CD的距离.

(1)在△ABD值中,因为在A处看灯塔B在货轮的北偏东75°的方向上,距离为12
海里,
24海里;货轮由A处向正北航行到D处时,再看灯塔B在南偏东60°方向上,
所以B=45°,由正弦定理
=
,
所以AD=
=
=24海里.
(2)在△ACD中,AD=24,AC=8
,∠CAD=30°,
由余弦定理可得:CD2=AD2+AC2-2•AD•ACcos30°=242+(8
)2-2×24×8
×
=192,
所以CD=8
海里.
| 6 |
24海里;货轮由A处向正北航行到D处时,再看灯塔B在南偏东60°方向上,
所以B=45°,由正弦定理
| AD |
| sinB |
| AB |
| sin∠ADB |
所以AD=
| AB•sinB |
| sin∠ADB |
12
| ||||||
|
(2)在△ACD中,AD=24,AC=8
| 3 |
由余弦定理可得:CD2=AD2+AC2-2•AD•ACcos30°=242+(8
| 3 |
| 3 |
| ||
| 2 |
所以CD=8
| 3 |

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 某货轮在A处看灯塔B在货轮的北偏东75°的方向上,距离为
某货轮在A处看灯塔B在货轮的北偏东75°的方向上,距离为 如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离
如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离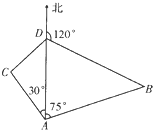 如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离为12
如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离为12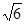 海里,在A处看灯塔已在货轮的北偏西30°,距离为8
海里,在A处看灯塔已在货轮的北偏西30°,距离为8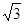 海里,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求:
海里,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求: