题目内容
某货轮在A处看灯塔B在货轮北偏东75°,距离为12| 6 |
| 3 |
(Ⅰ)A处与D处之间的距离;
(Ⅱ)灯塔C与D处之间的距离.
分析:(Ⅰ)利用已知条件,利用正弦定理求得AD的长.
(Ⅱ)在△ADC中由余弦定理可求得CD,答案可得.
(Ⅱ)在△ADC中由余弦定理可求得CD,答案可得.
解答:解:(Ⅰ)在△ABD中,由已知得∠ADB=60°,B=45°
由正弦定理得AD=
=
=24
(Ⅱ)在△ADC中,由余弦定理得CD2=AD2+AC2-2AD•ACcos30°,解得CD=8
.
所以A处与D处之间的距离为24nmile,灯塔C与D处之间的距离为8
nmile.
由正弦定理得AD=
| ABsinB |
| sinADB |
12
| ||||||
|
(Ⅱ)在△ADC中,由余弦定理得CD2=AD2+AC2-2AD•ACcos30°,解得CD=8
| 3 |
所以A处与D处之间的距离为24nmile,灯塔C与D处之间的距离为8
| 3 |
点评:本题主要考查了解三角形的实际应用.解题的关键是根据题意建立适当的三角函数模型,利用正弦定理,余弦定理等常用公式来求解.

练习册系列答案
相关题目
 某货轮在A处看灯塔B在货轮的北偏东75°的方向上,距离为
某货轮在A处看灯塔B在货轮的北偏东75°的方向上,距离为 如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离
如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离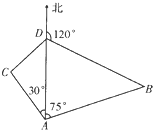 如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离为12
如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离为12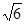 海里,在A处看灯塔已在货轮的北偏西30°,距离为8
海里,在A处看灯塔已在货轮的北偏西30°,距离为8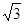 海里,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求:
海里,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求: