题目内容
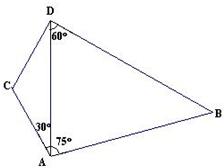
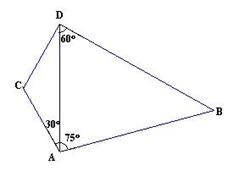
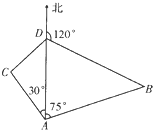 如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离为12
如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离为12| 6 |
| 3 |
(I)货船的航行速度
(Ⅱ)灯塔C与D之间的距离(精确到1nmile).
分析:(I)在三角形ABD中,利用正弦定理列出关系式,将各自的值代入求出AD的长,即可确定出货船的航行速度;
(Ⅱ)在三角形ACD中,利用余弦定理列出关系式,将各自的值代入计算即可求出CD的长.
(Ⅱ)在三角形ACD中,利用余弦定理列出关系式,将各自的值代入计算即可求出CD的长.
解答: 解:(Ⅰ)在△ABD中,∠ADB=60°,∴∠B=45°,
解:(Ⅰ)在△ABD中,∠ADB=60°,∴∠B=45°,
由正弦定理,得
=
,
即AD=
=
=24(nmile),
则货船的航行速度为V=
=12nmile/h;
(Ⅱ)在△ACD中,∵AC=8
,∠CAD=30°,
∴由余弦定理得CD2=AD2+AC2-2AD•ACcos∠CAD=242+(8
)2-2×24×8
cos30°=192,
解得:CD=8
≈14(nmile),
则灯塔C与D之间的距离约为14nmile.
 解:(Ⅰ)在△ABD中,∠ADB=60°,∴∠B=45°,
解:(Ⅰ)在△ABD中,∠ADB=60°,∴∠B=45°,由正弦定理,得
| AD |
| sinB |
| AB |
| sin∠ADB |
即AD=
| ABsinB |
| sin∠ADB |
12
| ||||||
|
则货船的航行速度为V=
| 24 |
| 2 |
(Ⅱ)在△ACD中,∵AC=8
| 3 |
∴由余弦定理得CD2=AD2+AC2-2AD•ACcos∠CAD=242+(8
| 3 |
| 3 |
解得:CD=8
| 3 |
则灯塔C与D之间的距离约为14nmile.
点评:此题考查了正弦定理,余弦定理,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
 如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离
如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离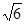 海里,在A处看灯塔已在货轮的北偏西30°,距离为8
海里,在A处看灯塔已在货轮的北偏西30°,距离为8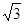 海里,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求:
海里,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求: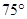 ,距离为
,距离为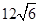 海里,在A处看灯塔C在货轮的北偏西
海里,在A处看灯塔C在货轮的北偏西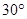 ,距离为
,距离为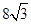 海里。货轮由A处向正北方向航行到D处时,再看灯塔B在南偏东
海里。货轮由A处向正北方向航行到D处时,再看灯塔B在南偏东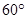
 (1) A处与D处的距离;
(1) A处与D处的距离;