题目内容
在由y=0,y=2,x=0,x=π四条直线围成的区域内任取一点,这点没落在y=sinx和x轴所围成区域内的概率是
1-
| 1 |
| π |
1-
.| 1 |
| π |
分析:作出图象,由定积分可得阴影面积,所求概率为空白面积与矩形面积的比值,代入几何概型可得.
解答: 解:(如图),可得矩形的面积为2π,
解:(如图),可得矩形的面积为2π,
阴影部分的面积为
sinxdx=-cosx
=2,
∴点没落在y=sinx和x轴所围成区域内的概率P=
=1-
故答案为:1-
 解:(如图),可得矩形的面积为2π,
解:(如图),可得矩形的面积为2π,阴影部分的面积为
| ∫ | π 0 |
| | | π 0 |
∴点没落在y=sinx和x轴所围成区域内的概率P=
| 2π-2 |
| 2π |
| 1 |
| π |
故答案为:1-
| 1 |
| π |
点评:本题考查几何概型的求解,涉及定积分求面积,属中档题.

练习册系列答案
相关题目
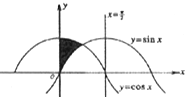 如图,在由x=0,y=0,x=
如图,在由x=0,y=0,x=| π |
| 2 |
A、1-
| ||||
B、
| ||||
C、
| ||||
D、3-2
|
 对t∈R恒成立,求m的取值范围.
对t∈R恒成立,求m的取值范围.