题目内容
等差数列{an}中，a4+a5+a6+a7+a8=150，则S11= ．
考点：等差数列的性质,等差数列的前n项和
专题：等差数列与等比数列
分析：由等差数列的性质可知，项数之和相等的两项之和相等且等于项数之和一半的项，把已知条件化简后，即可求出a5的值，然后再由等差数列前n项和公式求出前11项的和S11．
解答：
等差数列 {an}中，a4+a5+a6+a7+a8=150，
所以5a6=150，
所以a6=30，
所以S11=
=11a6=330．
则前11项的和S11=330．
故答案为：330．
所以5a6=150，
所以a6=30，
所以S11=
| (a1+a11)×11 |
| 2 |
则前11项的和S11=330．
故答案为：330．
点评：题考查学生灵活运用等差数列的性质化简求值，同时考查等差数列的前n项和公式，是一道中档题．
练习册系列答案
相关题目
函数y=log2x的反函数和y=log2
的反函数的图象关于（ ）
| 1 |
| x |
| A、x轴对称 | B、y轴对称 |
| C、y=x对称 | D、原点对称 |
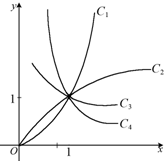如图是幂函数y=xn在第一象限内的图象，已知n取| 1 |
| 2 |
| 1 |
| 2 |
A、2，
| ||||
B、-2，-
| ||||
C、-
| ||||
D、2，
|
若a=0.32，b=20.3，c=log0.32，则a，b，c由大到小的关系是（ ）
| A、a＞b＞c |
| B、b＞a＞c |
| C、b＞c＞a |
| D、c＞a＞b |