题目内容
16.向量$\overrightarrow{a}$=(2,-1,3),$\overrightarrow{b}$=(-4,2,x),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则x=$\frac{10}{3}$;若$\overrightarrow{a}$与$\overrightarrow{b}$夹角是锐角,则x 的取值范围$(\frac{10}{3},+∞)$.分析 ①由$\overrightarrow{a}$⊥$\overrightarrow{b}$,可得$\overrightarrow{a}•\overrightarrow{b}$=-8-2+3x=0,解得x.
②由$\overrightarrow{a}$与$\overrightarrow{b}$夹角是锐角,可得$\overrightarrow{a}•\overrightarrow{b}$=-8-2+3x>0,解得x范围.若$\overrightarrow{a}∥\overrightarrow{b}$,则$\overrightarrow{a}=λ\overrightarrow{b}$,可得$\left\{\begin{array}{l}{2=-4λ}\\{-1=2λ}\\{3=xλ}\end{array}\right.$,解得x,进而得出范围.
解答 解:①∵$\overrightarrow{a}$⊥$\overrightarrow{b}$,则$\overrightarrow{a}•\overrightarrow{b}$=-8-2+3x=0,解得x=$\frac{10}{3}$.
②∵$\overrightarrow{a}$与$\overrightarrow{b}$夹角是锐角,∴$\overrightarrow{a}•\overrightarrow{b}$=-8-2+3x>0,解得x>$\frac{10}{3}$.
若$\overrightarrow{a}∥\overrightarrow{b}$,则$\overrightarrow{a}=λ\overrightarrow{b}$,∴$\left\{\begin{array}{l}{2=-4λ}\\{-1=2λ}\\{3=xλ}\end{array}\right.$,解得x=-6<$\frac{10}{3}$.
∴$\overrightarrow{a}$与$\overrightarrow{b}$夹角是锐角,则x 的取值范围是$(\frac{10}{3},+∞)$.
故答案为:$\frac{10}{3}$;$(\frac{10}{3},+∞)$.
点评 本题考查了向量数量积运算性质、向量夹角公式、向量共线定理,考查了推理能力与计算能力,属于中档题.

| A. | P⊆Q | B. | Q⊆P | C. | P∈Q | D. | Q∈P |
| A. | [2,3] | B. | [2,3) | C. | {2,3} | D. | {2} |
| A. | $0<a≤\frac{π}{2}$ | B. | $0<a≤\frac{π}{12}$ | ||
| C. | $a=kπ+\frac{π}{12},k∈{N^*}$ | D. | $2kπ<a≤2kπ+\frac{π}{12},k∈N$ |
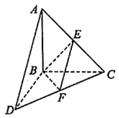 如图,三棱锥A-BCD中,△ABC和△BCD所在平面互相垂直,且AB=CD=4,AC=4$\sqrt{2}$,CD=4$\sqrt{3}$,∠ACB=45°,E,F分别为MN的中点.
如图,三棱锥A-BCD中,△ABC和△BCD所在平面互相垂直,且AB=CD=4,AC=4$\sqrt{2}$,CD=4$\sqrt{3}$,∠ACB=45°,E,F分别为MN的中点.