题目内容
已知椭圆 的离心率
的离心率 ,长轴的左右端点分别为
,长轴的左右端点分别为 ,
, .
.
(1)求椭圆 的方程;
的方程;
(2)设动直线 与曲线
与曲线 有且只有一个公共点
有且只有一个公共点 ,且与直线
,且与直线 相交于点
相交于点 .问在
.问在 轴上是否存在定点
轴上是否存在定点 ,使得以
,使得以 为直径的圆恒过定点
为直径的圆恒过定点 ,若存在,求出
,若存在,求出 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
 的离心率
的离心率 ,长轴的左右端点分别为
,长轴的左右端点分别为 ,
, .
.(1)求椭圆
 的方程;
的方程;(2)设动直线
 与曲线
与曲线 有且只有一个公共点
有且只有一个公共点 ,且与直线
,且与直线 相交于点
相交于点 .问在
.问在 轴上是否存在定点
轴上是否存在定点 ,使得以
,使得以 为直径的圆恒过定点
为直径的圆恒过定点 ,若存在,求出
,若存在,求出 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.(1)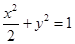 ;(2)存在,
;(2)存在,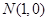
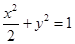 ;(2)存在,
;(2)存在,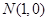
试题分析:(1)由已知,得
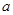 ,再根据离心率求
,再根据离心率求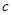 ,进而求
,进而求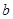 ,进而根据焦点位置求椭圆方程;(2)联立直线方程和椭圆方程,得关于
,进而根据焦点位置求椭圆方程;(2)联立直线方程和椭圆方程,得关于 的一元二次方程,由题意
的一元二次方程,由题意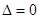 ,列方程得
,列方程得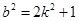 ,同时可求出切点坐标
,同时可求出切点坐标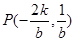 ,再求
,再求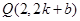 ,设
,设 轴上存在满足条件的点
轴上存在满足条件的点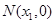 ,以
,以 为直径的圆恒过定点
为直径的圆恒过定点 等价于
等价于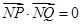 ,列方程得
,列方程得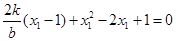 ,由题意该方程与
,由题意该方程与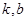 无关,故
无关,故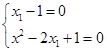 ,从而求得
,从而求得 点坐标,本题还可以先从特殊值入手,确定定点
点坐标,本题还可以先从特殊值入手,确定定点 的坐标,再证明以
的坐标,再证明以 为直径的圆恒过定点
为直径的圆恒过定点 .
.试题解析:(1)由已知
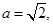
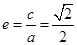 2分
2分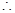
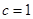 ,
,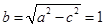
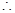 椭圆
椭圆 的方程为
的方程为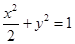 ; 4分
; 4分(2)
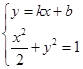 ,消去
,消去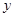 ,得
,得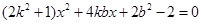 ,则
,则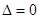 ,可得
,可得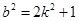 ,设切点
,设切点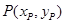 ,则
,则 ,
,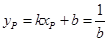 ,故
,故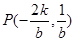 ,又由
,又由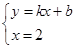 ,得
,得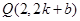 ,设在
,设在 上存在定点
上存在定点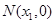 ,使得以
,使得以 为直径的圆恒过定点,
为直径的圆恒过定点,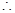
 ,即
,即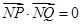 10分
10分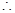
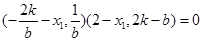 ,
,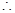
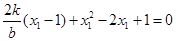 对满足
对满足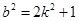 恒成立,
恒成立,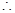
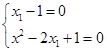 ,
,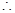
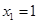
故在
 轴上存在定点
轴上存在定点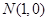 ,使得以
,使得以 为直径的圆恒过定点
为直径的圆恒过定点 . 14分
. 14分
练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 的一个顶点和两个焦点构成的三角形的面积为4.
的一个顶点和两个焦点构成的三角形的面积为4. 的方程;
的方程; 与椭圆
与椭圆 、
、 两点,试问,是否存在
两点,试问,是否存在 轴上的点
轴上的点 ,使得对任意的
,使得对任意的 ,
, 为定值,若存在,求出
为定值,若存在,求出 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由. 是椭圆
是椭圆 的一个顶点,
的一个顶点, 的长轴是圆
的长轴是圆 的直径,
的直径, 、
、 是过点
是过点 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中 于
于 、
、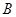 两点,
两点,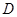 .
.
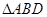 面积的最大值及取得最大值时直线
面积的最大值及取得最大值时直线 与抛物线
与抛物线 的焦点重合,过
的焦点重合,过

 与椭圆相交于不同两点A和B,且满足
与椭圆相交于不同两点A和B,且满足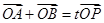 (O为坐标原点),求实数t的取值范围.
(O为坐标原点),求实数t的取值范围. (a>b>0)的上、下顶点分别为A、B,已知点B在直线l:
(a>b>0)的上、下顶点分别为A、B,已知点B在直线l: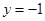 上,且椭圆的离心率e =
上,且椭圆的离心率e =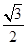 .
.
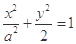 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,则该椭圆的离心率是( )
的焦点重合,则该椭圆的离心率是( )

 的左焦点为
的左焦点为 与过原点的直线相交于
与过原点的直线相交于 两点,连接
两点,连接 ,若
,若 ,则椭圆
,则椭圆 的离心率
的离心率




 的双曲线和离心率为
的双曲线和离心率为 的椭圆有相同的焦点
的椭圆有相同的焦点 、
、 ,
, 是两曲线的一个公共点,若
是两曲线的一个公共点,若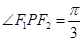 ,则
,则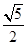
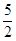


 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为 .不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
.不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.