题目内容
已知定义在R+上的函数f(x)单调递减,且对任意x∈(0,+∞)恒有f(f(x)-log
x)=1,则函数f(x)的零点为( )
| 1 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |
考点:函数单调性的性质,对数的运算性质
专题:函数的性质及应用
分析:设f(x)-log
x=t,则方程等价为f(t)=1,然后令x=t,即可求出t的值,然后利用零点求解的方法,即可得到结论.
| 1 |
| 2 |
解答:
解:设f(x)-log
x=t,则f(x)=log
x+t
方程等价为f(t)=1,
令x=t,则f(t)=log
t+t=1,解得t=1,
∵函数f(x)单调递减,
∴t值唯一,
∴f(x)=log
x+1,
由f(x)=log
x+1=0得log
x=-1,
解得x=2,
故选:C.
| 1 |
| 2 |
| 1 |
| 2 |
方程等价为f(t)=1,
令x=t,则f(t)=log
| 1 |
| 2 |
∵函数f(x)单调递减,
∴t值唯一,
∴f(x)=log
| 1 |
| 2 |
由f(x)=log
| 1 |
| 2 |
| 1 |
| 2 |
解得x=2,
故选:C.
点评:本题主要考查函数零点的求解,根据函数的单调性求出函数的表达式是解决本题的关键.综合性较强,有一点的难度.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
执行如图所示的程序框图,若输入的x的值为3,则输出的y的值为( )
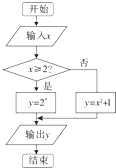

| A、4 | B、5 | C、8 | D、10 |
复数z=1+
的模为( )
| 1 |
| i |
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
设a,b,c,d∈R,则“a>b,c>d”是“ac>bd”成立的 ( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
计算sin15°sin75°+cos15°cos75°=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将函数y=sin(2x-θ)的图象F向右平移
个单位长度得到图象F′,若F′的一个对称中心是(
π,0),则θ的一个可能取值是( )
| π |
| 6 |
| 3 |
| 8 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|