题目内容
下列函数中,定义域是R且为增函数的是( )
| A、y=e-x | ||
| B、y=x | ||
| C、y=lnx | ||
D、y=-
|
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:根据题意,对选项中的函数进行认真分析,选出符合条件的答案来.
解答:
解:对于选项C定义域为(0,+∞),选项D定义域为(-∞,0)∪(0,+∞),故CD不符合,
对于A,y=e-x为减函数,故A不符合,
函数y=x的k=1>0,定义域是R且为增函数,故B符合;
故选:B.
对于A,y=e-x为减函数,故A不符合,
函数y=x的k=1>0,定义域是R且为增函数,故B符合;
故选:B.
点评:本题考查了基本初等函数的定义域和单调性问题,解题时应对选项中的函数进行分析,从而选出正确的答案,是基础题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列四个命题:
①若m⊥α,m⊥β,则α∥β;
②若α⊥γ,β⊥γ,则α∥β;
③若m?α,n?β,m∥n,则α∥β;
④若m、n是异面直线,m?α,m∥β,n?β,n∥α,则α∥β.
其中正确的是( )
①若m⊥α,m⊥β,则α∥β;
②若α⊥γ,β⊥γ,则α∥β;
③若m?α,n?β,m∥n,则α∥β;
④若m、n是异面直线,m?α,m∥β,n?β,n∥α,则α∥β.
其中正确的是( )
| A、①和② | B、①和③ |
| C、③和④ | D、①和④ |
下列函数中,在其定义域内为减函数的是( )
| A、y=-x3 | ||
B、y=x
| ||
| C、y=x2 | ||
| D、y=log2x |
在四边形ABCD中,若
+
=0,
•
=0,则四边形为( )
| AB |
| CD |
| AC |
| BD |
| A、平行四边形 | B、矩形 |
| C、等腰梯形 | D、菱形 |
若点(a,4)在函数y=2x的图象上,则cos
的值为( )
| aπ |
| 3 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
如果f(x)为偶函数,满足在区间[2,3]上是增函数且最小值是4,那么f(x)在区间[-3,-2]上是( )
| A、增函数且最小值是-4 |
| B、增函数且最大值是4 |
| C、减函数且最小值是4 |
| D、减函数且最大值是-4 |
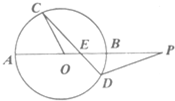 如图;圆O的割线PA过圆心O交圆于另一点B,弦CD交OB于点E,且△COE~△POE,PB=OA=2,则PE的长等于( )
如图;圆O的割线PA过圆心O交圆于另一点B,弦CD交OB于点E,且△COE~△POE,PB=OA=2,则PE的长等于( )