题目内容
【题目】在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数).在以
为参数).在以![]() 为极点、
为极点、![]() 轴的非负半轴为极轴的极坐标系(两种坐标系的单位长度相同)中,曲线
轴的非负半轴为极轴的极坐标系(两种坐标系的单位长度相同)中,曲线![]() :
:![]() 的焦点
的焦点![]() 的极坐标为
的极坐标为![]() .
.
(1)求常数![]() 的值;
的值;
(2)设![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() ,求
,求![]() 的大小.
的大小.
【答案】(1)8;(2)![]() 或
或![]() .
.
【解析】
(1)曲线C的极坐标方程化为直角坐标方程知曲线C为抛物线,焦点![]() 的极坐标方程转化为直角坐标方程即可求得
的极坐标方程转化为直角坐标方程即可求得![]() ;(2)将直线
;(2)将直线![]() 的参数方程代入
的参数方程代入![]() 整理得到关于t的一元二次方程,根据韦达定理用
整理得到关于t的一元二次方程,根据韦达定理用![]() 表示出
表示出![]() 、
、![]() ,由
,由![]() 得
得![]() ,三个方程联立即可求出
,三个方程联立即可求出![]() .
.
(1)曲线![]() 方程可化为
方程可化为![]() ,其直角坐标方程为
,其直角坐标方程为![]() .
.
又焦点![]() 的直角坐标为
的直角坐标为![]() ,
,
所以![]() ,解得
,解得![]() .
.
(2)将直线![]() 的参数方程代入
的参数方程代入![]() ,并整理得
,并整理得![]() ,
,
其中![]() 恒成立,且
恒成立,且![]() ①,
①,![]() ②,
②,
由![]() 得
得![]() ,结合①得
,结合①得![]() ,
,![]() .
.
代入②得![]() ,解得
,解得![]() .
.
又因为![]() ,所以
,所以![]() 的大小为
的大小为![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
18 | |||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: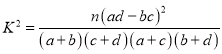 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
【题目】某手机商家为了更好地制定手机销售策略,随机对顾客进行了一次更换手机时间间隔的调查.从更换手机的时间间隔不少于3个月且不超过24个月的顾客中选取350名作为调查对象,其中男性顾客和女性顾客的比为![]() ,商家认为一年以内(含一年)更换手机为频繁更换手机,否则视为未频繁更换手机.现按照性别采用分层抽样的方法从中抽取105人,并按性别分为两组,得到如下表所示的频数分布表:
,商家认为一年以内(含一年)更换手机为频繁更换手机,否则视为未频繁更换手机.现按照性别采用分层抽样的方法从中抽取105人,并按性别分为两组,得到如下表所示的频数分布表:
事件间隔(月) |
|
|
|
|
|
|
|
男性 | x | 8 | 9 | 18 | 12 | 8 | 4 |
女性 | y | 2 | 5 | 13 | 11 | 7 | 2 |
(1)计算表格中x,y的值;
(2)若以频率作为概率,从已抽取的105且更换手机时间间隔为3至6个月(含3个月和6个月)的顾客中,随机抽取2人,求这2人均为男性的概率;
(3)请根据频率分布表填写![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“频繁更换手机与性别有关”.
以上的把握认为“频繁更换手机与性别有关”.
频繁更换手机 | 未频繁更换手机 | 合计 | |
男性顾客 | |||
女性顾客 | |||
合计 |
附表及公式:
P( | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |