题目内容
19.已知直线l:(k-1)x-2y+5-3k=0(k∈R)恒过定点P,圆C经过点A(4,0)和点P,且圆心在直线x-2y+1=0上.(1)求定点P的坐标;
(2)求圆C的方程;
(3)已知点P为圆C直径的一个端点,若另一个端点为点Q,问:在y轴上是否存在一点M(0,m),使得△PMQ为直角三角形,若存在,求出m的值,若不存在,请说明理由.
分析 (1)左右直线l的方程:k(x-3)-(x+2y-5)=0,令$\left\{\begin{array}{l}x-3=0\\ x+2y-5=0\end{array}\right.$,即可求得定点P的坐标;
(2)设圆的方程,由题意列方程组,即可求圆的标准方程;
(3)由(2)可知:求得直线CP的斜率,根据对称性求得Q点坐标,由M在圆外,所以点M不能作为直角三角形的顶点,分类讨论,即可求得m的值.
解答 解:(1)由(k-1)x-2y+5-3k=0得,k(x-3)-(x+2y-5)=0,
令$\left\{\begin{array}{l}x-3=0\\ x+2y-5=0\end{array}\right.$,得$\left\{\begin{array}{l}x=3\\ y=1\end{array}\right.$,即定点P的坐标为(3,1).
(2)设圆C的方程为x2+y2+Dx+Ey+F=0,
由条件得$\left\{\begin{array}{l}16+4D+F=0\\ 9+1+3D+E+F=0\\({-\frac{D}{2}})-2({-\frac{E}{2}})+1=0\end{array}\right.$,解得$\left\{\begin{array}{l}D=-14\\ E=-8\\ F=40\end{array}\right.$.
所以圆C的方程为x2+y2-14x-8y+40=0,
圆C的标准方程(x-7)2+(y-4)2=25.
(3)圆C的标准方程为(x-7)2+(y-4)2=25,则${k_{CP}}=\frac{4-1}{7-3}=\frac{3}{4}$,
设点P(3,1)关于圆心(7,4)的对称点为(x0,y0),则有$\left\{\begin{array}{l}3+{x_0}=14\\ 1+{y_0}=8\end{array}\right.$,
解得x0=11,y0=7,故点Q的坐标为(11,7).
因为M在圆外,所以点M不能作为直角三角形的顶点,
若点P为直角三角形的顶点,则有$\frac{m-1}{0-3}•\frac{3}{4}=-1$,m=5,
若点Q是直角三角形的顶点,则有$\frac{m-7}{0-11}•\frac{3}{4}=-1$,$m=\frac{65}{3}$,
综上,m=5或$\frac{65}{3}$.
点评 本题考查圆的标准方程的求法,直线与椭圆的位置关系,考查分类讨论思想,属于中档题.

| A. | 150o | B. | 60o | C. | 120o | D. | 30o |
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
10 10 10 9 10 8 8 10 10 8.
| A. | 0.81 | B. | 0.9 | C. | 0.64 | D. | 0.8 |
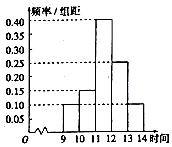 一商场在某日促销活动中,对9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售为( )
一商场在某日促销活动中,对9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售为( )| A. | 100万元 | B. | 10万元 | C. | 7.5万元 | D. | 6.25万元 |
| A. | a>0,4a+b=0 | B. | a<0,4a+b=0 | C. | a>0,2a+b=0 | D. | a<0,2a+b=0 |
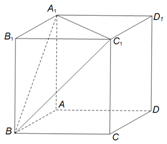 如图,在棱长为2的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=6,则点P的轨迹所形成的图形的面积是( )
如图,在棱长为2的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=6,则点P的轨迹所形成的图形的面积是( )| A. | 2π | B. | $\frac{11π}{2}$ | C. | $\frac{16π}{3}$ | D. | $\frac{52π}{9}$ |