题目内容
10.若f(x)=-$\frac{1}{2}$x2+mlnx在(1,+∞)是减函数,则m的取值范围是( )| A. | [1,+∞) | B. | (1,+∞) | C. | (-∞,1] | D. | (-∞,1) |
分析 求出函数的导数,通过讨论m的范围讨论函数的单调性,从而确定m的范围即可.
解答 解:f(x)=-$\frac{1}{2}$x2+mlnx,
f′(x)=-x+$\frac{m}{x}$=$\frac{{-x}^{2}+m}{x}$,
m≤0时,f′(x)<0,f(x)在(0,+∞)递减,符合题意,
m>0时,只需-x2+m≤0在x∈(1,+∞)恒成立即可,
即m≤x2≤1,
综上:m≤1,
故选:C.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
20.不等式x-2y+3>0表示的区域在直线x-2y+3=0的( )
| A. | 右上方 | B. | 右下方 | C. | 左上方 | D. | 左下方 |
1.命题:?x∈Z,x2∈Z的否定是命题( )
| A. | ?x∈Z,x2∉Z | B. | ?x∉Z,x2∉Z | C. | ?x∈Z,x2∈Z | D. | ?x∈Z,x2∉Z |
15.已知函数f(x)=ax-1+4的图象恒过定点P,则点P的坐标是( )
| A. | (1,5) | B. | (1,4) | C. | (0,4) | D. | (4,0) |
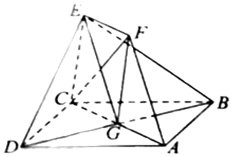 (理)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.
(理)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.