题目内容
(本小题满分14分)已知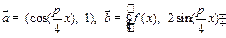 ,
,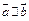 . 数列
. 数列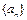 满足
满足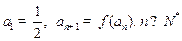 .
.
(Ⅰ)证明: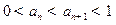 ;
;
(Ⅱ)已知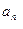 ≥
≥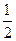 ,证明:
,证明: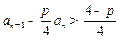 ;
;
(Ⅲ)设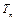 是数列
是数列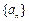 的前
的前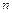 项和,判断
项和,判断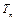 与
与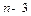 的大小,并说明理由.
的大小,并说明理由.
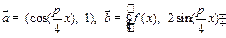 ,
,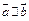 . 数列
. 数列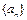 满足
满足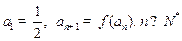 .
.(Ⅰ)证明:
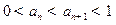 ;
;(Ⅱ)已知
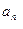 ≥
≥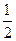 ,证明:
,证明: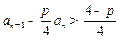 ;
;(Ⅲ)设
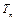 是数列
是数列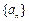 的前
的前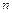 项和,判断
项和,判断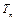 与
与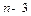 的大小,并说明理由.
的大小,并说明理由. 略
解:(I)∵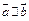 ,∴
,∴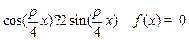 .
.
∴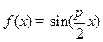 . ∴
. ∴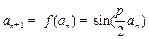 . (1分)
. (1分)
下面用数学归纳法证明: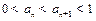 .
.
①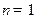 时,
时,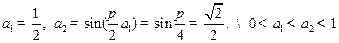 ,故结论成立.
,故结论成立.
②假设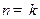 时结论成立,即
时结论成立,即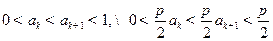 .
.
∴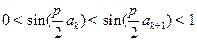 ,即
,即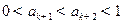 .
.
也就是说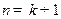 时,结论也成立.
时,结论也成立.
由①②可知,对一切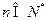 均有
均有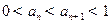 . (4分)
. (4分)
(Ⅱ)要证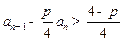 ,即证
,即证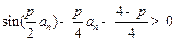 ,其中
,其中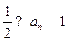 .
.
令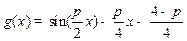 .
. 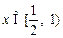 .
.
由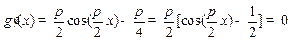 ,得
,得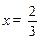 . (6分)
. (6分)
又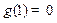 ,
,
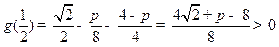 .
.
∴当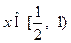 ,
,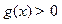 .
.
∴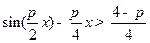 .
.
∴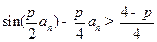 . 即
. 即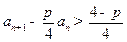 . (9分)
. (9分)
(Ⅲ)由(Ⅱ)知:
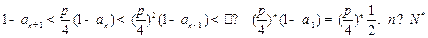 . (11分)
. (11分)
∴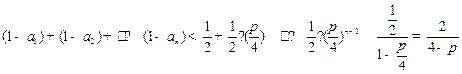 .
.
∴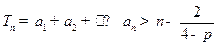 . (13分)
. (13分)
又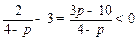 ,即
,即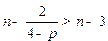 .
.
∴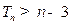 . (14分)
. (14分)
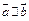 ,∴
,∴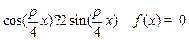 .
.∴
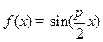 . ∴
. ∴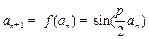 . (1分)
. (1分)下面用数学归纳法证明:
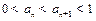 .
.①
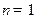 时,
时,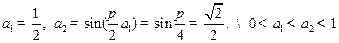 ,故结论成立.
,故结论成立.②假设
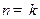 时结论成立,即
时结论成立,即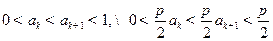 .
.∴
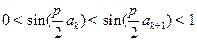 ,即
,即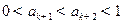 .
.也就是说
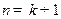 时,结论也成立.
时,结论也成立.由①②可知,对一切
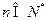 均有
均有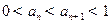 . (4分)
. (4分)(Ⅱ)要证
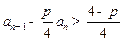 ,即证
,即证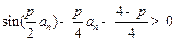 ,其中
,其中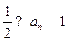 .
.令
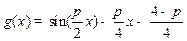 .
. 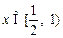 .
.由
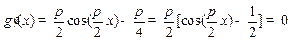 ,得
,得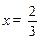 . (6分)
. (6分)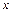 | 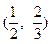 | 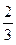 | 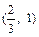 |
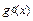 | + | 0 | — |
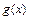 | 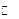 | 极大值 | 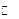 |
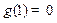 ,
, 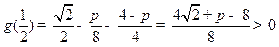 .
.∴当
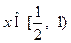 ,
,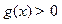 .
. ∴
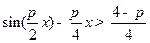 .
. ∴
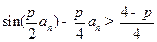 . 即
. 即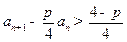 . (9分)
. (9分)(Ⅲ)由(Ⅱ)知:
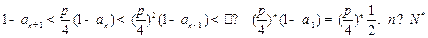 . (11分)
. (11分)∴
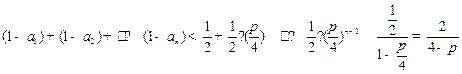 .
.∴
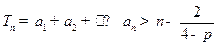 . (13分)
. (13分)又
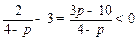 ,即
,即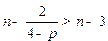 .
.∴
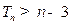 . (14分)
. (14分)
练习册系列答案
相关题目
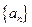 的前
的前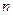 项和为
项和为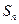 ,对
,对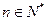 ,都有
,都有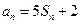 成立,
成立,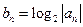 ,试
,试 求数列
求数列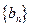 的前
的前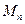
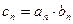 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.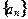 满足:
满足: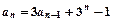
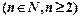 ,其中
,其中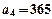 ,
,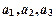 ;
;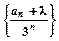 为等差数列,求常数
为等差数列,求常数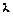 的值;
的值; 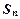 。
。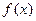 ,若存在
,若存在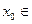 R,使
R,使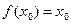 成立,则称
成立,则称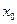 为
为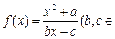 N*
N*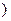 有且仅有两个不动点0和2,且
有且仅有两个不动点0和2,且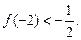
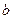 ,
,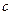 的值;
的值;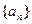
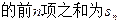 ,并且
,并且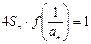 , 求数列
, 求数列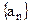 的通项公式;;
的通项公式;;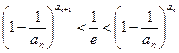 .
.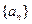 满足递推式:
满足递推式: 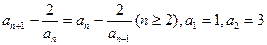
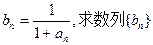 的通项公式;
的通项公式;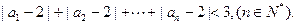
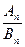 =
=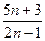 ,则
,则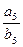 =
=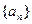 的前n项和为
的前n项和为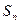 ,令
,令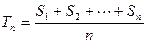 ,称
,称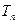 为数列
为数列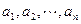 的“理想数”,已知数列
的“理想数”,已知数列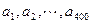 的“理想数”为2005,则
的“理想数”为2005,则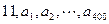 的“理想数”为
的“理想数”为