题目内容
6.已知函数f(x)=loga(1-$\frac{a}{x}$),其中0<a<1.(1)证明:f(x)是(a,+∞)上的减函数;
(2)若f(x)=1,求x;
(3)若f(x)>1,求x的取值范围.
分析 (1)利用不等式性质得出1$-\frac{a}{{x}_{1}}$$<1-\frac{a}{{x}_{2}}$.利用对数函数的单调性,结合复合函数loga(1-$\frac{a}{{x}_{1}}$)>loga(1-$\frac{a}{{x}_{2}}$).即f(x1)>f(x2).判断即可.
(2)根据对数运算得出loga(1-$\frac{a}{x}$)=1.即1-$\frac{a}{x}$=a.求解即可得出x的值.
(3)利用对数函数的单调性得出loga(1-$\frac{a}{x}$)>1,其中0<a<1.0<1-$\frac{a}{x}$<1,其中0<a<1,求解不等式得出x的范围.
解答 解:函数f(x)=loga(1-$\frac{a}{x}$),其中0<a<1.
(1)设x1,x2∈(a,+∞)上,且x1<x2.
∴1>$\frac{a}{{x}_{1}}$$>\frac{a}{{x}_{2}}$.1$-\frac{a}{{x}_{1}}$$<1-\frac{a}{{x}_{2}}$.
∵0<a<1.
∴loga(1-$\frac{a}{{x}_{1}}$)>loga(1-$\frac{a}{{x}_{2}}$)
即f(x1)>f(x2)
∴f(x)是(a,+∞)上的减函数;
(2)∵f(x)=1.
∴loga(1-$\frac{a}{x}$)=1.
即1-$\frac{a}{x}$=a.
x=$\frac{a}{1-a}$
(3)∵f(x)>1,
∴loga(1-$\frac{a}{x}$)>1,其中0<a<1.
0<1-$\frac{a}{x}$<1,其中0<a<1.
求解得出:x>a.
点评 本题综合考察了对数函数的性质运算,结合函数的单调性,不等式求解,属于综合题目,注意参数a的值的限制.

| A. | 2 | B. | 3 | C. | 4 | D. | 2$\sqrt{2}$ |
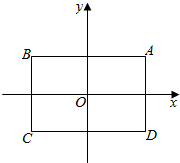 如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分是点A,B的对应点,$\frac{A′B′}{AB}$=k.已知关于x,y的元二次一次方程$\left\{\begin{array}{l}{mnx+y=3n+1}\\{3x+y=4}\end{array}\right.$(m,n是实数)无解,在以m,n为坐标(记为m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上.则k•t的值等于1.
如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分是点A,B的对应点,$\frac{A′B′}{AB}$=k.已知关于x,y的元二次一次方程$\left\{\begin{array}{l}{mnx+y=3n+1}\\{3x+y=4}\end{array}\right.$(m,n是实数)无解,在以m,n为坐标(记为m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上.则k•t的值等于1.