题目内容
11.设函数f(x)对任意x,y∈R,都有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,又f(1)=-2.(I)求f(0)的值; (II)求证:f(x)是奇函数;
(III)当-3≤x≤3时,不等式f(x)≤2m-1恒成立,求m的取值范围.
分析 (I)由f(x)+f(y)=f(x+y),令x=y=0,解得f(0).
(II)令y=-x,则f(x)+f(-x)=f(0)=0,即可证明.
(III)任取-3≤x1<x2≤3,则f(x2)=f(x1+x2-x1)=f(x1)+f(x2-x1),利用当x>0时,f(x)<0,
即可得出f(x)在[-3,3]上是减函数.可得f(x)在[-3,3]上的最大值为f(3).由f(1)=-2,可得f(2)=2f(1),f(3)=f(2)+f(1).当-3≤x≤3时,不等式f(x)≤2m-1恒成立,f(x)max≤2m-1,即可得出.
解答 (I)解:由f(x)+f(y)=f(x+y),
令x=y=0,则2f(0)=f(0),解得f(0)=0.
(II)证明:令y=-x,则f(x)+f(-x)=f(0)=0,
∴f(-x)=-f(x).
∴f(x)在[-1,1]上的奇函数.
(III)解:任取-3≤x1<x2≤3,则f(x2)=f(x1+x2-x1)=f(x1)+f(x2-x1),
由x2-x1>0,∴f(x2-x1)<0,∴f(x2)<f(x1),
∴f(x)在[-3,3]上是减函数.
∴f(x)在[-3,3]上的最大值为f(3).
∵f(1)=-2,∴f(2)=2f(1)=-4,
f(3)=f(2)+f(1)=-4-2=-6.
当-3≤x≤3时,不等式f(x)≤2m-1恒成立,
∴f(x)max≤2m-1,∴-6≤2m-1,解得m≥$-\frac{5}{2}$.
∴m的取值范围是$[-\frac{5}{2},+∞)$.
点评 本题考查了抽象函数的单调性与奇偶性、不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知数列{an},它的前n项和为Sn,若an=$\frac{1}{(2n+1)(2n-1)}$,则Sn=( )
| A. | $\frac{2}{2n+1}$ | B. | $\frac{2n}{2n+1}$ | C. | $\frac{n}{2n+1}$ | D. | $\frac{1}{2n+1}$ |
20.点P是椭圆$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}$=1上一点,F1,F2分别是椭圆的左、右焦点,若|PF1||PF2|=12,则∠F1PF2的大小为( )
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
1.已知f(x)=$\left\{\begin{array}{l}{2^{1-x}},x≤1\\ 1-{log_2}^x,x>1\end{array}$则满足f(x)≤2的x取值范围是( )
| A. | [-1,2] | B. | [0,2] | C. | [1,+∞) | D. | [0,+∞) |
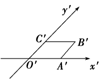 在直观图(如图所示)中,四边形O'A'B'C'为菱形且边长为2cm,则在xOy坐标系中,四边形OABC的面积为8cm2.
在直观图(如图所示)中,四边形O'A'B'C'为菱形且边长为2cm,则在xOy坐标系中,四边形OABC的面积为8cm2.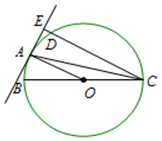 如图所示,BC 为⊙O 的直径,$\widehat{AB}=\widehat{AD}$,以点 A 为切点的切线与 CD 的延长线交于点E
如图所示,BC 为⊙O 的直径,$\widehat{AB}=\widehat{AD}$,以点 A 为切点的切线与 CD 的延长线交于点E