题目内容
已知函数 ,若f(x0)<3,则x0的取值范围是________.
,若f(x0)<3,则x0的取值范围是________.
(-∞,0)∪(0,8)
分析:分x≤0和x>0两种情况求解.x0≤0时,f(x0)= <3;x0>0时,f(x0)=log2x0<3,分别求解,再求并集即可求得x0的取值范围.
<3;x0>0时,f(x0)=log2x0<3,分别求解,再求并集即可求得x0的取值范围.
解答:x0≤0时,f(x0)= <3,则x0<1,
<3,则x0<1,
f(x0)=log2x0<3,解得0<x0<8
所以x0的范围为x0<1或0<x0<8
故答案为:(-∞,0)∪(0,8).
点评:本题考查分段函数、解不等式、指数函数、对数函数等基础知识,体现了分类讨论的思想,属中档题.
分析:分x≤0和x>0两种情况求解.x0≤0时,f(x0)=
 <3;x0>0时,f(x0)=log2x0<3,分别求解,再求并集即可求得x0的取值范围.
<3;x0>0时,f(x0)=log2x0<3,分别求解,再求并集即可求得x0的取值范围.解答:x0≤0时,f(x0)=
 <3,则x0<1,
<3,则x0<1,f(x0)=log2x0<3,解得0<x0<8
所以x0的范围为x0<1或0<x0<8
故答案为:(-∞,0)∪(0,8).
点评:本题考查分段函数、解不等式、指数函数、对数函数等基础知识,体现了分类讨论的思想,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,若f(x0)=8,则x0=________.
,若f(x0)=8,则x0=________. ,若f(x0)=12,则x0=________.
,若f(x0)=12,则x0=________. ,若f(x0)≥2,则x0的取值范围是________.
,若f(x0)≥2,则x0的取值范围是________.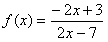 ,若存在实数x0,使f(x0)=x0,则称x0是函数y=f(x)的一个不动点,
,若存在实数x0,使f(x0)=x0,则称x0是函数y=f(x)的一个不动点,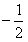 且x≠
且x≠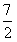 时,比较
时,比较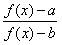 与
与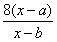 的大小;
的大小; 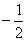 且an≠
且an≠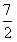 ,a1=1,等式an+1=f(an)对任何正整数n都成立,求数列{an}的通项公式。
,a1=1,等式an+1=f(an)对任何正整数n都成立,求数列{an}的通项公式。