题目内容
已知函数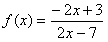 ,若存在实数x0,使f(x0)=x0,则称x0是函数y=f(x)的一个不动点,
,若存在实数x0,使f(x0)=x0,则称x0是函数y=f(x)的一个不动点,
(Ⅰ)求函数y=f(x)的不动点;
(Ⅱ)已知a、b是y=f(x)的两个不动点,且a>b,当x≠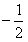 且x≠
且x≠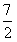 时,比较
时,比较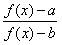 与
与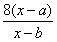 的大小;
的大小;
(Ⅲ)在数列{an}中,an≠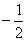 且an≠
且an≠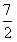 ,a1=1,等式an+1=f(an)对任何正整数n都成立,求数列{an}的通项公式。
,a1=1,等式an+1=f(an)对任何正整数n都成立,求数列{an}的通项公式。
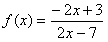 ,若存在实数x0,使f(x0)=x0,则称x0是函数y=f(x)的一个不动点,
,若存在实数x0,使f(x0)=x0,则称x0是函数y=f(x)的一个不动点,(Ⅰ)求函数y=f(x)的不动点;
(Ⅱ)已知a、b是y=f(x)的两个不动点,且a>b,当x≠
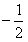 且x≠
且x≠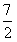 时,比较
时,比较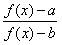 与
与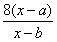 的大小;
的大小; (Ⅲ)在数列{an}中,an≠
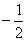 且an≠
且an≠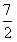 ,a1=1,等式an+1=f(an)对任何正整数n都成立,求数列{an}的通项公式。
,a1=1,等式an+1=f(an)对任何正整数n都成立,求数列{an}的通项公式。 解:(Ⅰ)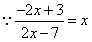 ,
,
∴ ,∴
,∴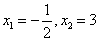 ,
,
经过检验,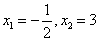 是方程的解,
是方程的解,
∴函数y=f(x)有两上不动点,它们是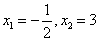 。
。
(Ⅱ)由(Ⅰ)可知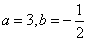 ,
,
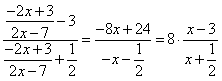 ,
,
∴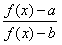 与
与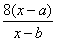 相等。
相等。
(Ⅲ)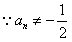 且
且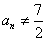 ,由(Ⅱ)知
,由(Ⅱ)知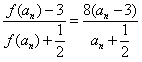 ,
,
∴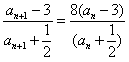 ,
,
∴数列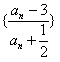 是以
是以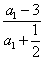 为首项,8为公比的等比数列,
为首项,8为公比的等比数列,
即以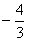 为首项,8为公比的等比数列,
为首项,8为公比的等比数列,
∴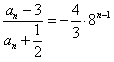 ,
,
∴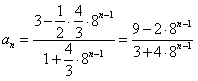 。
。
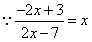 ,
,∴
 ,∴
,∴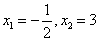 ,
,经过检验,
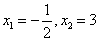 是方程的解,
是方程的解,∴函数y=f(x)有两上不动点,它们是
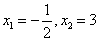 。
。(Ⅱ)由(Ⅰ)可知
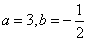 ,
,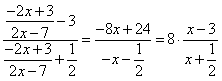 ,
,∴
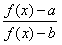 与
与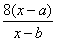 相等。
相等。 (Ⅲ)
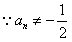 且
且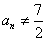 ,由(Ⅱ)知
,由(Ⅱ)知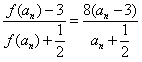 ,
,∴
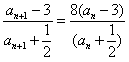 ,
,∴数列
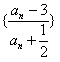 是以
是以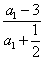 为首项,8为公比的等比数列,
为首项,8为公比的等比数列,即以
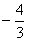 为首项,8为公比的等比数列,
为首项,8为公比的等比数列,∴
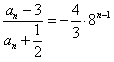 ,
,∴
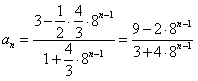 。
。 
练习册系列答案
相关题目
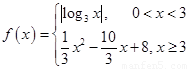 ,若存在实数
,若存在实数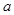 、
、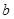 、
、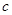 、
、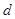 ,满足
,满足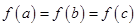
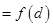 ,其中
,其中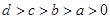 ,则
,则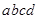 的取值范围是
.
的取值范围是
.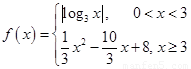 ,若存在实数
,若存在实数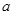 、
、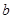 、
、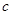 、
、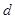 ,满足
,满足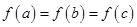
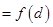 ,其中
,其中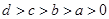 ,则
,则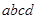 的取值范围是
.
的取值范围是
.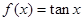 有无数个零点;
有无数个零点;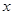 的方程
的方程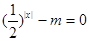 有解,则实数
有解,则实数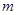 的取值范围是
的取值范围是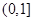 ;
;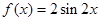 的图象沿
的图象沿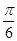 个单位后,得到的函数解析式可以表示成
个单位后,得到的函数解析式可以表示成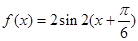 ;
;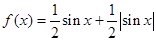 的值域是
的值域是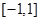 ;
;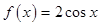 ,若存在实数
,若存在实数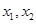 ,使得对任意的实数
,使得对任意的实数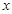 都有
都有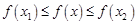 成立,则
成立,则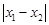 的最小值为
的最小值为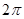 。
。 ,若存在实数
,若存在实数 则称
则称 是函数
是函数 的一个不动点.
的一个不动点. .当
.当 时,比较
时,比较 的大小;
的大小; 中,
中, ,等式
,等式 对任何正整数n都成立,求数列
对任何正整数n都成立,求数列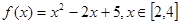 ,若存在实数
,若存在实数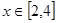 使
使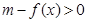 成立,则
成立,则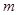 的取值范围为(**** )
的取值范围为(**** )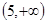 B.
B.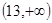
 C.
C.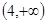 D.
D.