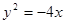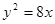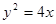题目内容
(本小题满分12分)
已知椭圆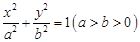 的离心率
的离心率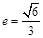 ,过点
,过点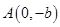 和
和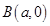 的直线与原点的距离为
的直线与原点的距离为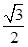 。⑴求椭圆的方程;⑵已知定点
。⑴求椭圆的方程;⑵已知定点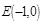 ,若直线
,若直线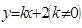 与椭圆交于
与椭圆交于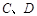 两点,问:是否存在
两点,问:是否存在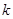 的值,使以
的值,使以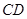 为直径的圆过
为直径的圆过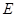 点?请说明理由。
点?请说明理由。
已知椭圆
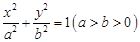 的离心率
的离心率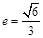 ,过点
,过点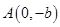 和
和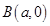 的直线与原点的距离为
的直线与原点的距离为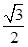 。⑴求椭圆的方程;⑵已知定点
。⑴求椭圆的方程;⑵已知定点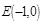 ,若直线
,若直线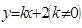 与椭圆交于
与椭圆交于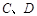 两点,问:是否存在
两点,问:是否存在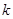 的值,使以
的值,使以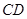 为直径的圆过
为直径的圆过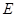 点?请说明理由。
点?请说明理由。(1)椭圆的方程为 ;(2)存在
;(2)存在 使得以CD为直径的圆过点E。
使得以CD为直径的圆过点E。
 ;(2)存在
;(2)存在 使得以CD为直径的圆过点E。
使得以CD为直径的圆过点E。试题分析:(1)直线
 方程为
方程为
依题意可得:
 解得:
解得:
∴椭圆的方程为

(2)假设存在这样的值。
由
 得
得
∴

设

而

要使以
 为直径的圆过点
为直径的圆过点 ,当且仅当
,当且仅当 时
时则

即


将(2)代入(3)整理得

经验证
 使得(1)成立
使得(1)成立综上可知,存在
 使得以CD为直径的圆过点E。
使得以CD为直径的圆过点E。点评:圆锥曲线的问题一般来说计算量大,对运算能力要求很高,寻求简洁、合理的运算途径很重要,在解答时注意以下的转化:⑴若直线与圆锥曲线有两个交点,对待交点坐标是“设而不求”的原则,要注意应用韦达定理处理这类问题 ; ⑵与弦的重点有关问题求解常用方法一韦达定理法 二 点差法;

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 上一点
上一点 到其焦点
到其焦点 的距离等于4,则
的距离等于4,则
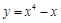 上点
上点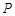 处的切线平行于直线
处的切线平行于直线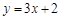 ,那么点
,那么点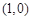
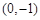
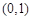
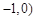
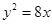 的焦点,M的离心率
的焦点,M的离心率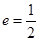 ,过M的右焦点F作不与坐标轴垂直的直线
,过M的右焦点F作不与坐标轴垂直的直线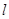 ,交M于A,B两点。
,交M于A,B两点。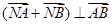 ,求实数t的取值范围。
,求实数t的取值范围。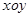 中,点
中,点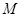 到两定点F1
到两定点F1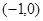 和F2
和F2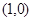 的距离之和为
的距离之和为 ,设点
,设点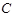 .(1)求曲线
.(1)求曲线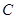 的方程; (2)若直线
的方程; (2)若直线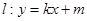 与曲线
与曲线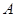 、
、 (
(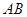 为直径的圆过点
为直径的圆过点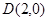 ,试判断直线
,试判断直线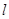 是否经过一定点,若是,求出定点坐标;若不是,说明理由.
是否经过一定点,若是,求出定点坐标;若不是,说明理由.
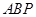 的顶点
的顶点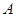 、
、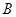 分别为双曲线
分别为双曲线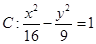 的左右焦点,顶点
的左右焦点,顶点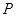 在双曲线
在双曲线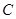 上,则
上,则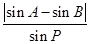 的值等于
的值等于 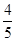
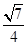
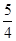
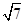
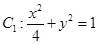 ,椭圆
,椭圆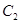 以
以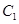 的长轴为短轴,且与
的长轴为短轴,且与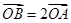 ,求直线
,求直线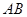 的方程.
的方程.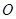 ,焦点在
,焦点在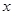 轴上,两条渐近线分别为
轴上,两条渐近线分别为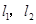 ,经过右焦点
,经过右焦点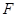 垂直于
垂直于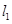 的直线分别交
的直线分别交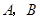 两点.已知
两点.已知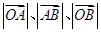 成等差数列,且
成等差数列,且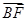 与
与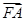 同向.
同向.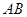 被双曲线所截得的线段的长为4,求双曲线的方程.
被双曲线所截得的线段的长为4,求双曲线的方程.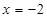 ,则抛物线方程是( )
,则抛物线方程是( )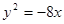 ,
,