题目内容
如图（1）、（2）、（3）、（4）四个图案，每个图案都是由小正方形拼成，现按同样的规律 （小正方形的摆放规律相同）进行拼图，设第n个图形包含f（n）个小正方形．（1）f（6）=
考点：归纳推理
专题：计算题,推理和证明
分析：先分别观察给出正方体的个数为：1，1+4，1+4+8，…总结一般性的规律，将一般性的数列转化为特殊的数列再求解．
解答：
解：因为f（2）-f（1）=4=4×1，
f（3）-f（2）=8=4×2，
f（4）-f（3）=12=4×3，
f（5）-f（4）=16=4×4，
…
由上式规律，所以得出f（n+1）-f（n）=4n．
因为f（n+1）-f（n）=4n，
所以f（n+1）=f（n）+4n，
f（n）=f（n-1）+4（n-1）
=f（n-2）+4（n-1）+4（n-2）
=f（n-3）+4（n-1）+4（n-2）+4（n-3）
=…
=f（1）+4（n-1）+4（n-2）+4（n-3）+…+4
=2n2-2n+1．
所以f（6）=61．
故答案为：61；2n2-2n+1．
f（3）-f（2）=8=4×2，
f（4）-f（3）=12=4×3，
f（5）-f（4）=16=4×4，
…
由上式规律，所以得出f（n+1）-f（n）=4n．
因为f（n+1）-f（n）=4n，
所以f（n+1）=f（n）+4n，
f（n）=f（n-1）+4（n-1）
=f（n-2）+4（n-1）+4（n-2）
=f（n-3）+4（n-1）+4（n-2）+4（n-3）
=…
=f（1）+4（n-1）+4（n-2）+4（n-3）+…+4
=2n2-2n+1．
所以f（6）=61．
故答案为：61；2n2-2n+1．
点评：本题主要考查归纳推理，其基本思路是先分析具体，观察，总结其内在联系，得到一般性的结论，若求解的项数较少，可一直推理出结果，若项数较多，则要得到一般求解方法，再求具体问题．
练习册系列答案
相关题目
如图，边长为3的正方形ABCD中，点E，F分别为边AB，BC上的点，将△AED，△DCF分别沿DE，DF折起，使A，C两点重合于点A′．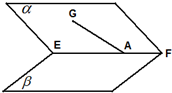
平面角为锐角的二面角α-EF-β，A∈EF，AG?α，∠GAE=45°，若AG与β所成角为30°，则二面角α-EF-β的大小是