题目内容
已知f(x)=3x-3|x|,若3tf(2t)-mf(t)≥0对于t∈[-2,-1]恒成立,则m∈ .
考点:函数恒成立问题
专题:函数的性质及应用
分析:由已知得f(x)=3x-3|x|在(-∞,0)上单调递增,f(t)=3t-3-t<0,m≤-32t-1,令g(t)=-32t-1,则g(t)在[-2,-1]上递减,由此能求出实数m的取值范围.
解答:
解:∵y=3x在(-∞,0)上单调递增,y=3|x|在(-∞,0)上单调递减,
∴f(x)=3x-3|x|在(-∞,0)上单调递增,
∵t∈[-2,-1],∴f(t)=3t-3-t<0,
∴3tf(2t)-mf(t)≥0化为:
3t(32t-3-2t)+m(3t-3-t)≥0,
即3t(3t+3-t)+m≤0,即m≤-32t-1,
令g(t)=-32t-1,则g(t)在[-2,-1]上递减,
∴g(x)mim=g(-1)=-3-2-1=-
,
∴m≤g(x)min=-
∴所求实数m的取值范围是(-∞,-
].
故答案为:(-∞,-
].
∴f(x)=3x-3|x|在(-∞,0)上单调递增,
∵t∈[-2,-1],∴f(t)=3t-3-t<0,
∴3tf(2t)-mf(t)≥0化为:
3t(32t-3-2t)+m(3t-3-t)≥0,
即3t(3t+3-t)+m≤0,即m≤-32t-1,
令g(t)=-32t-1,则g(t)在[-2,-1]上递减,
∴g(x)mim=g(-1)=-3-2-1=-
| 10 |
| 9 |
∴m≤g(x)min=-
| 10 |
| 9 |
∴所求实数m的取值范围是(-∞,-
| 10 |
| 9 |
故答案为:(-∞,-
| 10 |
| 9 |
点评:本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
| ∫ | e 1 |
| 1 |
| x |
A、
| ||
B、1-
| ||
| C、1 | ||
| D、e-1 |
已知实数a,b,c,d成等比数列,且曲线y=3x-x3的极大值点坐标为(b,c)则ad等于( )
| A、2 | B、1 | C、-1 | D、-2 |
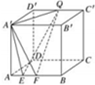 如图,正方体ABCD-A′B′C′D′的棱长为4,动点E,F在棱AB上,且EF=2,动点Q在棱D′C′上,则三棱锥A′-EFQ的体积( )
如图,正方体ABCD-A′B′C′D′的棱长为4,动点E,F在棱AB上,且EF=2,动点Q在棱D′C′上,则三棱锥A′-EFQ的体积( )| A、与点E,F位置有关 |
| B、与点Q位置有关 |
| C、与点E,F,Q位置有关 |
| D、与点E,F,Q位置均无关,是定值 |