Question

如图，左侧的是一个长方体截去一个角所得多面体的直观图，它的正视图和侧视图如图（单位：cm）．
（1）求该多面体的体积；
（2）证明：平面BDC′∥平面EFG．

Answer 1

分析：（1）利用转化思想V=V_长方体-V_正三棱锥，求该多面体的体积；
（2）在长方体ABCD-A′B′C′D′中，连接AD′，在所给直观图中连接BC′，证明EG∥BC′，即可证明BC′∥面EFG，同理BD∥平面EFG，即可证明平面BDC′∥平面EFG．

解答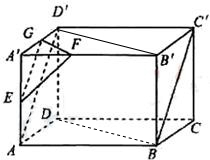：解：（1）由题意，多面体可以看成一个长方体截去一个小三棱锥，
∴所求多面体体积V=V_长方体-V_正三棱锥=4×4×6-

1

3

×(

1

2

×2×2)×2=

284

3

（cm³）．…（6分）
（2）证明：补全长方体ABCD-A′B′C′D′中，依题意E，G分别为AA′，A′D′的中点．
连接BD，B′D′，则四边形AD′C′B为平行四边形，
∴AD′∥BC′．…（9分）
∵E，G分别为AA′，A′D′的中点，
∴AD′∥EG，从而EG∥BC′．
∵EG?平面EFG，BC′?平面EFG，
∴BC′∥平面EFG．…（12分）
同理BD∥平面EFG．
∵BC′∩BD=B，
∴平面BDC′∥平面EFG．…（14分）

点评：本题考查几何体体积的计算，考查面面平行，考查学生分析解决问题的能力，属于中档题．