题目内容
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).(1)求函数f(t)解析式;
(2)画出函数y=f(t)的图象;
(3)当函数g(t)=f(t)-at有且只有一个零点时,求a的值.

【答案】分析:(1)利用分段函数,求函数f(t)的解析式.
(2)利用(1)的解析式作出函数的图象.(3)求出g(t)=f(t)-at的表达式,利用g(t)=f(t)-at有且只有一个零点时,求a的值.
解答: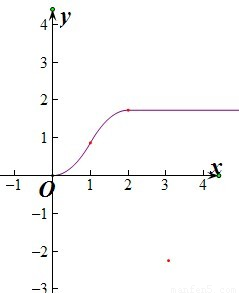 解:(1)当0<t≤1时,
解:(1)当0<t≤1时,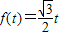 2 (1分)
2 (1分)
当1<t≤2时,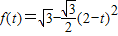 (2分)
(2分)
当t>2时,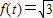 (3分)
(3分)
所以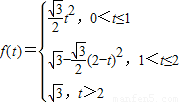 (4分)
(4分)
(2)画图象(4分),如图:(其中图形(3分),规范1分)
(3)当0<t≤1时,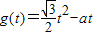 ,由
,由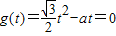 ,解得
,解得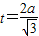
因为0<t≤1,所以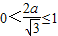 ,即
,即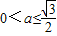 (9分)
(9分)
当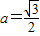 时,直线y=at过点
时,直线y=at过点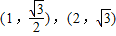 ,这两点都在f(t)的图象上
,这两点都在f(t)的图象上
当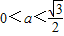 时,直线y=at与射线
时,直线y=at与射线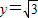 有一个交点 (10分)
有一个交点 (10分)
当1<t≤2时,直线y=a(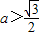 )逆时针旋转时与f(t)图象有两个交点,相切时有一个交点,且与射线
)逆时针旋转时与f(t)图象有两个交点,相切时有一个交点,且与射线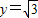 无交点.(11分)
无交点.(11分)
此时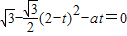 ,所以
,所以 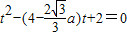 ,
,
所以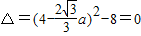 ,解得
,解得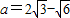 或
或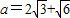 .(12分)
.(12分)
当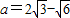 时,
时,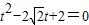 ,所以
,所以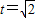 在(1,2]内.
在(1,2]内.
当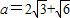 .时
.时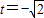 不在(1,2]内,(13分)
不在(1,2]内,(13分)
当a≤0或a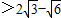 时,直线y=at与f(t)的图象无交点
时,直线y=at与f(t)的图象无交点
所以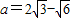 .(14分)
.(14分)
点评:本题主要考查了分段函数的求法以及函数零点的应用,综合性较强,运算量较大.
(2)利用(1)的解析式作出函数的图象.(3)求出g(t)=f(t)-at的表达式,利用g(t)=f(t)-at有且只有一个零点时,求a的值.
解答:
 解:(1)当0<t≤1时,
解:(1)当0<t≤1时,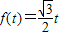 2 (1分)
2 (1分)当1<t≤2时,
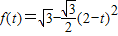 (2分)
(2分)当t>2时,
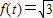 (3分)
(3分)所以
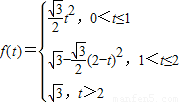 (4分)
(4分)(2)画图象(4分),如图:(其中图形(3分),规范1分)
(3)当0<t≤1时,
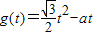 ,由
,由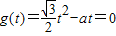 ,解得
,解得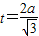
因为0<t≤1,所以
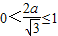 ,即
,即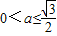 (9分)
(9分)当
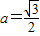 时,直线y=at过点
时,直线y=at过点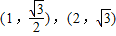 ,这两点都在f(t)的图象上
,这两点都在f(t)的图象上当
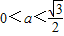 时,直线y=at与射线
时,直线y=at与射线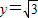 有一个交点 (10分)
有一个交点 (10分)当1<t≤2时,直线y=a(
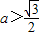 )逆时针旋转时与f(t)图象有两个交点,相切时有一个交点,且与射线
)逆时针旋转时与f(t)图象有两个交点,相切时有一个交点,且与射线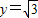 无交点.(11分)
无交点.(11分)此时
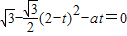 ,所以
,所以 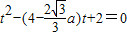 ,
,所以
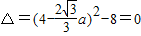 ,解得
,解得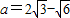 或
或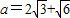 .(12分)
.(12分)当
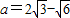 时,
时,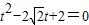 ,所以
,所以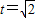 在(1,2]内.
在(1,2]内.当
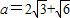 .时
.时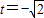 不在(1,2]内,(13分)
不在(1,2]内,(13分)当a≤0或a
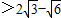 时,直线y=at与f(t)的图象无交点
时,直线y=at与f(t)的图象无交点所以
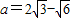 .(14分)
.(14分)点评:本题主要考查了分段函数的求法以及函数零点的应用,综合性较强,运算量较大.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
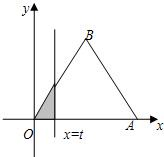 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).试求函数f(t)的解析式,并画出函数y=f(t)的图象.
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).试求函数f(t)的解析式,并画出函数y=f(t)的图象. 如图,△OAB是边长为1的等边三角形,直线x=t截这个三角形位于此直线左方的图形面积(图中阴影部分)为y,求函数y=f(t)的解析式.
如图,△OAB是边长为1的等边三角形,直线x=t截这个三角形位于此直线左方的图形面积(图中阴影部分)为y,求函数y=f(t)的解析式. 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t). 如图,△OAB是边长为4的正三角形,记△OAB位于直线x=t(0<t<6)左侧的图形的面积为f(t),试求f(t)的解析式.
如图,△OAB是边长为4的正三角形,记△OAB位于直线x=t(0<t<6)左侧的图形的面积为f(t),试求f(t)的解析式. (2010•武汉模拟)如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积f(t),则函数f(t)的解析式为:
(2010•武汉模拟)如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积f(t),则函数f(t)的解析式为: