题目内容
19.若x,y满足约束条件$\left\{\begin{array}{l}{x≤1}\\{x-y+1≥0}\\{x+2y-2≥0}\end{array}\right.$,则z=x2+y2的最小值为$\frac{4}{5}$.分析 作出不等式组对应的平面区域,利用z的几何意义进行求解即可.
解答 解:作出x,y满足约束条件$\left\{\begin{array}{l}{x≤1}\\{x-y+1≥0}\\{x+2y-2≥0}\end{array}\right.$,对应的平面区域如图,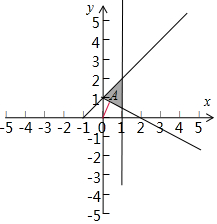
z的几何意义为区域内的点到原点的距离的平方,
由图象知:
OA的距离最小,
则|OA|2=$(\frac{|-2|}{\sqrt{{1}^{2}+{2}^{2}}})^{2}$=$\frac{4}{5}$,
故z=x2+y2的最小值为:$\frac{4}{5}$,
故答案为:$\frac{4}{5}$.
点评 本题主要考查线性规划的应用以及两点间的距离公式的应用,利用数形结合是解决本题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
10.下列说法正确的是( )
| A. | 若$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|-|{\overrightarrow b}|$,则$\overrightarrow a⊥\overrightarrow b$ | |
| B. | 若a,b,c为实数,且a<b<0,则$\frac{b}{a}<\frac{a}{b}$ | |
| C. | 已知m,n是空间两条不同的直线,α,β,γ是空间三个不同的平面,若α∩γ=m,β∩γ=n,m∥n则α∥β | |
| D. | 已知直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,若A1B2=A2B1,则l1∥l2 |
7.若角α的顶点为坐标原点,始边在x轴的非负半轴上,终边在直线$y=-\sqrt{3}x$上,则角α的取值集合是( )
| A. | $\{α|α=2kπ-\frac{π}{3},k∈Z\}$ | B. | $\{α|α=2kπ+\frac{2π}{3},k∈Z\}$ | C. | $\{α|α=kπ-\frac{2π}{3},k∈Z\}$ | D. | $\{α|α=kπ-\frac{π}{3},k∈Z\}$ |
4.为了解春季昼夜温差大小与种子发芽多少之间的关系,现从4月的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每50颗种子浸泡后的发芽数,得到如下表格:
(1)从这5天中任选2天,记发芽的种子数分别为m,n,求事件“m,n均小于13”的概率;
(2)若4月30日昼夜温差为6/oC,请根据y关于x的线性回归方程$\hat y=\hat bx+\hat a$估计该天种子浸泡后的发芽数.
参考公式:$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| 日期 | 4月1日 | 4月6日 | 4月12日 | 4月19日 | 4月27日 |
| 温差x/oC | 2 | 3 | 5 | 4 | 1 |
| 发芽数y/颗 | 9 | 11 | 15 | 13 | 7 |
(2)若4月30日昼夜温差为6/oC,请根据y关于x的线性回归方程$\hat y=\hat bx+\hat a$估计该天种子浸泡后的发芽数.
参考公式:$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.