题目内容
2.设集合S={0,1,2,3,5},从中任取两个不同的数作为A,B的值,得到直线Ax+By=0所有不同的直线的条数为多少?分析 通过对A、B中有无特殊数0进行分类讨论,计算即得结论.
解答 解:依题意,对A、B中有无特殊数0进行分类如下:
①当A、B中有一个为0时,此时只有直线x=0或y=0两条;
②当A、B中没有0时,此时有直线${A}_{4}^{2}$=12条;
由分类加法计数原理可知,共有2+12=14条.
点评 本题考查计数原理的应用,考查分类加法计数原理,注意解题方法的积累,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
13.设当x=θ时,函数f(x)=2cosx-3sinx取得最小值,则tanθ等于( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
14.用红、黄、蓝、绿4种颜色为一个五棱锥的六个顶点着色,要求每一条棱的两个端点着不同的颜色,则不同的着色方案共有 ( )种?
| A. | 120 | B. | 140 | C. | 180 | D. | 240 |
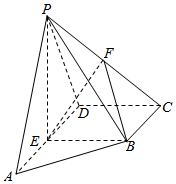 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,四边形ABCD为直角梯形,BC∥AD,∠ADC=90°,BC=CD=$\frac{1}{2}$AD=1,PA=PD,E,F分别为线段AD,PC的中点.
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,四边形ABCD为直角梯形,BC∥AD,∠ADC=90°,BC=CD=$\frac{1}{2}$AD=1,PA=PD,E,F分别为线段AD,PC的中点.