Question

【题目】已知函数，对于函数有下述四个结论：①函数在其定义域上为增函数；②对于任意的，，都有成立；③有且仅有两个零点；④若，则在点处的切线与在点处的切线为同一直线.其中所有正确的结论有( )

A.①②③B.①③C.②③④D.③④

Answer 1

【答案】C

【解析】

(1)分别求即可判定(1)错误.

(2)分别计算判断是否等于即可.

(3)数形结合分析函数与的交点个数即可.

(4)分别根据导数的几何意义求解在点处的切线与在点处的切线方程,再根据判定即可.

(1) 的定义域为.

因为,.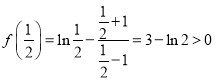

所以,所以在其定义域上不为增函数.故(1)错误.

(2)因为,.所以.

所以.故(2)正确.

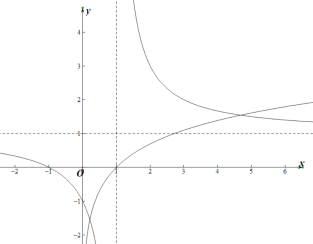
(3) 的零点即的解的个数,即函数与的交点个数.画出图像可知,有两个交点,故(3)正确.

(4)对于函数,因为,所以,所以在点处的切线方程为,即.

对于函数,,所以,

所以在处的切线方程为,

即.因为,即,其中且,

所以,.

所以.所以两条切线为同一直线.故(4)正确.

故选：C