题目内容
12．同时掷两个质地均匀的骰子，向上点数之积为12的概率是（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{9}$ | C． | $\frac{1}{18}$ | D． | $\frac{1}{36}$ |
分析 列举出可能的实验结果，根据古典概型概率计算公式计算．
解答 解：同时掷两个质地均匀的骰子，共有6×6=36种不同的结果，
其中向上点数之积为12的基本事件有（2，6），（3，4），（4，3），（6，2）共4个，
∴P=$\frac{4}{36}$=$\frac{1}{9}$．
故选B．
点评 本题考查了古典概型的概率计算，属于基础题．
练习册系列答案
相关题目
20．已知集合A={a，b，d}，B={c，d}，则A∪B等于（ ）
| A． | {d} | B． | {a，c} | C． | {a，b，c} | D． | {a，b，c，d} |
7．抛物线y2=2x的准线方程为（ ）
| A． | x=-1 | B． | x=-$\frac{1}{2}$ | C． | x=-$\frac{1}{4}$ | D． | x=$\frac{1}{2}$ |
17．
阅读右边的程序框图，运行相应的程序，输出的结果为（ ）
阅读右边的程序框图，运行相应的程序，输出的结果为（ ）| A． | 17 | B． | 10 | C． | 9 | D． | 5 |
16．设曲线y=xn+1（n∈Z*）在点（1，1）处的切线与x轴的交点的横坐标为xn，则x1•x2•x3…•xn的值为（ ）
| A． | $\frac{1}{n}$ | B． | $\frac{n}{n+1}$ | C． | $\frac{1}{n+1}$ | D． | 1 |
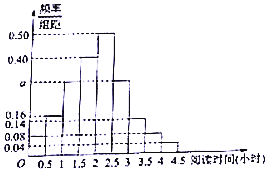某校为了解高一学生周末的“阅读时间”，从高一年级中随机调查了100名学生进行调查，获得了每人的周末“阅读时间”（单位：小时），按照[0，0.5），[0.5，1），…，[4，4.5]分成9组，制成样本的频率分布直方图如图所示．