题目内容
20.已知函数f(x)=x2-1,g(x)=x-1(1)若|f(x)|=ag(x)只有三个不同的解,求实数a的取值范围;
(2)若当x∈R时,不等式f(x)≥a|g(x)|恒成立,求实数a的取值范围;
(3)a∈(-∞,0],求函数h(x)=f(x)+a|g(x)|在[-2,2]上的最大值.
分析 (1)若|f(x)|=ag(x)只有三个不同的解,构造函数F(x)=|f(x)|,H(x)=ag(x)=ax-a,利用数形结合即可求实数a的取值范围;
(2)若当x∈R时,不等式f(x)≥a|g(x)|恒成立,利用参数分离法进行求解即可,求实数a的取值范围;
(3)根据绝对值的应用,将函数h(x)表示为复合函数形式,利用一元二次函数的性质进行求解即可.
解答 解:(1)∵|f(x)|=ag(x)只有三个不同的解,
令F(x)=|f(x)|,H(x)=ag(x)=ax-a,
做出函数F(x)的图象如图: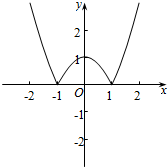
∵H(x)=ax-a过(1,0),
当a≥0时,显然不成立,
当a<0时,由图象知:-2<a<0,
∴实数a的取值范围为:-2<a<0;
(2)f(x)≥a|g(x)|恒成立,
∴(x+1)(x-1)≥a|x-1|,
当x≥1时,x+1≥a,则a≤2;
当x<1时,-x-1≥a,a≤-2;
故a的范围为a≤-2;
(3)当-2≤x≤1时,h(x)=)=f(x)+a|g(x)|=x2-1+a|x-1|=x2-1-ax+a=x2-ax+a-1,对称轴为x=-$\frac{-a}{2}$=$\frac{a}{2}$≤0,
当1≤x≤2时,h(x)=)=f(x)+a|g(x)|=x2-1+a|x-1|=x2-1+ax-a=x2+ax-(a+1),对称轴为x=$\frac{-a}{2}$=-$\frac{a}{2}$≥0,
∵h(1)=f(1)+a|g(1)|=0,
∴函数的最大值为max{h(2),h(-2)},
h(2)=4+2a-a-1=a+3,h(-2)=4+2a+a-1=3a+3,
∵a≤0,∴h(2)>h(-2),
即函数h(x)在在[-2,2]上的最大值为h(2)=a+3.
点评 本题主要考查不等式恒成立问题,利用参数分离法结合一元二次函数的单调性的性质是解决本题的关键.综合性较强,难度较大.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案①对于任意的x∈R,都有f(x+4)=f(x);
②对于任意的x1,x2∈R,且0≤x1<x2≤2,都有f(x1)<f(x2);
③函数y=f(x+2)的图象关于y轴对称
则下列结论中正确的是( )
| A. | f (4.5)<f (7)<f (6.5) | B. | f (7)<f (4.5)<f (6.5) | C. | f (7)<f (6.5)<f (4.5) | D. | f (4.5)<f (6.5)<f (7) |
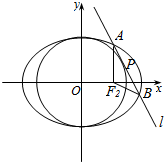 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{2}{3}$,F1、F2分别为其左、右焦点,点M为椭圆C的上的顶点,且,△MF1F2的面积为2$\sqrt{5}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{2}{3}$,F1、F2分别为其左、右焦点,点M为椭圆C的上的顶点,且,△MF1F2的面积为2$\sqrt{5}$.