题目内容
19.在△ABC中,已知向量$\overrightarrow{AB}$=(cos18°,cos72°),$\overrightarrow{BC}$=(2cos63°,2cos27°),则$|{\overrightarrow{AB}}|$=1,$|{\overrightarrow{BC}}|$=2,△ABC的面积为$\frac{\sqrt{2}}{2}$.分析 根据向量的模长=$\sqrt{{x}^{2}+{y}^{2}}$可得答案.在根据向量加减的运算求出$\overrightarrow{AC}$,可得|$\overrightarrow{AC}$|,即可求出三角形的面积.
解答 解:向量$\overrightarrow{AB}$=(cos18°,cos72°),$\overrightarrow{BC}$=(2cos63°,2cos27°),
则$|{\overrightarrow{AB}}|$=c=$\sqrt{co{s}^{2}18°+co{s}^{2}72°}=1$,
$|{\overrightarrow{BC}}|$=a=$\sqrt{4co{s}^{2}63°+4co{s}^{2}27°}=\sqrt{4}=2$,
∵$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$=(2cos63°+cos18°,2cos27°+cos72°)
可得|$\overrightarrow{AC}$|=b=$\sqrt{(2cos63°+cos18°)^{2}+(2cos27°+cos72°)^{2}}$)=$\sqrt{5+2\sqrt{2}}$
由余弦定理,可得cosB=-$\frac{\sqrt{2}}{2}$,则sinB=$\frac{\sqrt{2}}{2}$
则△ABC的面积S=$\frac{1}{2}$acsinB=$\frac{\sqrt{2}}{2}$.
故答案为:1,2,$\frac{\sqrt{2}}{2}$.
点评 本题考查了向量的模长的计算和向量加减的运算,以及三角形面积的求法.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+x+a,x<0}\\{-\frac{1}{x},x>0}\end{array}\right.$的图象上存在不同的两点A,B,使得曲线y=f(x)在这两点处的切线重合,则实数a的取值范围是( )
| A. | (-∞,$\frac{1}{4}$) | B. | (2,+∞) | C. | (-2,$\frac{1}{4}$) | D. | (-∞,2)∪($\frac{1}{4}$,+∞) |
4.函数y=xlnx的单调递增区间是( )
| A. | (-∞,e-1) | B. | (0,e-1) | C. | (e-1,+∞) | D. | (e,+∞) |
11.椭圆$\frac{x^2}{m}+\frac{y^2}{4}=1$的焦距为$2\sqrt{2}$,则m的值等于( )
| A. | 5或-3 | B. | 2或6 | C. | 5或3 | D. | $\sqrt{5}$或$\sqrt{3}$ |
9.在测试中,客观题难度的计算公式为Pi=$\frac{{R}_{i}}{N}$,其中Pi为第i题的难度,Ri为答对该题的人数,N为参加测试的总人数.
现对某校髙三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如表所示:
测试后,从中随机抽取了10名学生,将他们编号后统计各题的作答情况,如表所示(“√”表示答对,“×”表示答错):
(I)根据题中数据,将抽样的10名学生每道题实测的答对人数及相应的实测难度填入表,并估计这120名学生中第5题的实测答对人数;
(Ⅱ)从编号为1到5的5人中随机抽取2人,求恰好有1人答对第5题的概率;
(Ⅲ)定义统计量S=$\frac{1}{n}$[(P′1-P1)2+(P′2-P2)2+…+(P′n-Pn)2],其中P′i为第i题的实测难度,Pi为第i题的预估难度(i=l,2,…,n),规定:若S<0.05,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
现对某校髙三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如表所示:
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 考前预估难度Pi | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
| 题号 学生编号 | 1 | 2 | 3 | 4 | 5 |
| 1 | × | √ | √ | √ | √ |
| 2 | √ | √ | √ | √ | × |
| 3 | √ | √ | √ | √ | × |
| 4 | √ | √ | √ | × | × |
| 5 | √ | √ | √ | √ | √ |
| 6 | √ | × | × | √ | × |
| 7 | × | √ | √ | √ | × |
| 8 | √ | × | × | × | × |
| 9 | √ | √ | √ | × | × |
| 10 | √ | √ | √ | √ | × |
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 实测答对人数 | |||||
| 实测难度 |
(Ⅲ)定义统计量S=$\frac{1}{n}$[(P′1-P1)2+(P′2-P2)2+…+(P′n-Pn)2],其中P′i为第i题的实测难度,Pi为第i题的预估难度(i=l,2,…,n),规定:若S<0.05,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
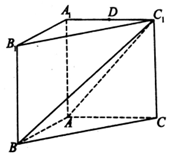 如图,直三棱柱ABC-A1B1C1中,AC=AA1=2AB,且BC1⊥A1C
如图,直三棱柱ABC-A1B1C1中,AC=AA1=2AB,且BC1⊥A1C