题目内容
14.设F1,F2是椭圆$\frac{x^2}{4}+{y^2}=1$的两个焦点,点P在椭圆上,且F1P⊥PF2,则△F1PF2的面积为1.分析 由已知得|PF1|+|PF2|=4,|F1F2|=2$\sqrt{3}$,由勾股定理得|PF1|•|PF2|=2,由此能求出△F1PF2的面积.
解答 解:∵F1,F2是椭圆$\frac{x^2}{4}+{y^2}=1$的两个焦点,点P在椭圆上,且F1P⊥PF2,
∴|PF1|+|PF2|=4,|F1F2|=2$\sqrt{3}$,
∴|PF1|2+|PF2|2+2|PF1|•|PF2|=16,
∴|F1F2|2+2|PF1|•|PF2|=16,
∴12+2|PF1|•|PF2|=16,
∴2|PF1|•|PF2|=4,∴|PF1|•|PF2|=2,
∴△F1PF2的面积S=$\frac{1}{2}$|PF1|•|PF2|=$\frac{1}{2}×2$=1.
故答案为:1.
点评 本题考查三角形的面积的求法,是基础题,解题时要认真审题,注意椭圆定义、勾股定理的合理运用.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
17.函数y=-2cos($\frac{x}{2}$+$\frac{π}{3}$)在区间($\frac{28}{5}$π,a]上是单调函数,则实数a的最大值为( )
| A. | $\frac{17π}{3}$ | B. | 6π | C. | $\frac{20π}{3}$ | D. | $\frac{22π}{3}$ |
19.以椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点F1,F2为直径的圆若和椭圆有交点,则椭圆离心率的取值范围是( )
| A. | $[\frac{{\sqrt{2}}}{2},1)$ | B. | $(\frac{{\sqrt{2}}}{2},1)$ | C. | $[\frac{{\sqrt{3}}}{2},1)$ | D. | $(\frac{{\sqrt{3}}}{2},1)$ |
6.P为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上异于左右顶点A1,A2的任意一点,则直线PA1与PA2的斜率之积为定值-$\frac{{b}^{2}}{{a}^{2}}$,将这个结论类比到双曲线,得出的结论为:P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上异于左右顶点A1,A2的任意一点,则( )
| A. | 直线PA1与PA2的斜率之和为定值$\frac{{a}^{2}}{{b}^{2}}$ | |
| B. | 直线PA1与PA2的斜率之积为定值$\frac{{a}^{2}}{{b}^{2}}$ | |
| C. | 直线PA1与PA2的斜率之和为定值$\frac{{b}^{2}}{{a}^{2}}$ | |
| D. | 直线PA1与PA2的斜率之积为定值$\frac{{b}^{2}}{{a}^{2}}$ |
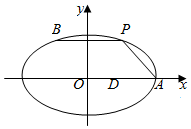 如图,在平面直角坐标系xOy中,已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点,点D(1,0),点P,B在椭圆上,且在x轴上方,$\overrightarrow{BP}$=$\overrightarrow{DA}$.
如图,在平面直角坐标系xOy中,已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点,点D(1,0),点P,B在椭圆上,且在x轴上方,$\overrightarrow{BP}$=$\overrightarrow{DA}$.