题目内容
2.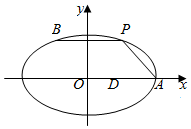 如图,在平面直角坐标系xOy中,已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点,点D(1,0),点P,B在椭圆上,且在x轴上方,$\overrightarrow{BP}$=$\overrightarrow{DA}$.
如图,在平面直角坐标系xOy中,已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点,点D(1,0),点P,B在椭圆上,且在x轴上方,$\overrightarrow{BP}$=$\overrightarrow{DA}$.(1)求直线BD的方程;
(2)已知抛物线C:x2=2py(p>0)过点P,点Q是抛物线C上的动点,设点Q到点A的距离为d1,点Q到抛物线C的准线的距离为d2,求d1+d2的最小值.
分析 (1)由已知得BP=DA=2,P(1,2),B(-1,2),由此能求出直线BD的方程.
(2)由已知求出p=$\frac{1}{4}$,d2=|QF|,从而当A、Q、F三点共线时,d1+d2有最小值.
解答 解:(1)∵BP=DA,且A(3,0),D(1,0),
∴BP=DA=2,而B、P关于y轴对称,
∴点P的横坐标为1,从而得到P(1,2),B(-1,2),
∴直线BD的方程为:$\frac{y}{x-1}=\frac{2}{-1-1}$,整理,得:x+y-1=0.
(2)∵抛物线C:x2=2py(P>0)过点P(1,2),
∴4p=1,即p=$\frac{1}{4}$,
∴抛物线C的焦点为F,则d2=|QF|,
∴当A、Q、F三点共线时,d1+d2有最小值,
即(d1+d2)min=|AF|=$\sqrt{{3}^{2}+(\frac{1}{8})^{2}}$=$\frac{\sqrt{577}}{8}$.
点评 本题考查直线方程的求法,考查两点间距离和点到抛物线的准线的距离之和的最小值的求法,是中档题,解题时要认真审题,注意椭圆性质和抛物线性质的合理运用.

练习册系列答案
相关题目
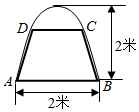 如图,有一块抛物线形钢板,其下口宽为2米,高为2米.计划将此钢板切割成等腰梯形的形状,下底AB是抛物线的下口,上底CD的端点在抛物线上.
如图,有一块抛物线形钢板,其下口宽为2米,高为2米.计划将此钢板切割成等腰梯形的形状,下底AB是抛物线的下口,上底CD的端点在抛物线上.