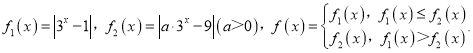题目内容
【题目】对于实数![]() ,将满足“
,将满足“![]() 且
且![]() 为整数”的实数
为整数”的实数![]() 称为实数
称为实数![]() 的小数部分,用记号
的小数部分,用记号![]() 表示.对于实数
表示.对于实数![]() ,无穷数列
,无穷数列![]() 满足如下条件:
满足如下条件:![]() ,
,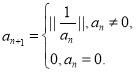 其中
其中![]() .
.
(1)若![]() ,求数列
,求数列![]() ;
;
(2)当![]() 时,对任意的
时,对任意的![]() ,都有
,都有![]() ,求符合要求的实数
,求符合要求的实数![]() 构成的集合
构成的集合![]() ;
;
(3)若![]() 是有理数,设
是有理数,设![]() (
(![]() 是整数,
是整数,![]() 是正整数,
是正整数,![]() 互质),问对于大于
互质),问对于大于![]() 的任意正整数
的任意正整数![]() ,是否都有
,是否都有![]() 成立,并证明你的结论.
成立,并证明你的结论.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)成立,证明见解析.
;(3)成立,证明见解析.
【解析】
试题分析:(1)利用新定义,可求数列![]() 的通项公式;(2)分类讨论,利用
的通项公式;(2)分类讨论,利用![]() ,即可求符合要求的实数
,即可求符合要求的实数![]() 构成的集合
构成的集合![]() ;(3)由
;(3)由![]() 是有理数,可知对一切正整数
是有理数,可知对一切正整数![]() ,
,![]() 为
为![]() 或正有理数,可设
或正有理数,可设![]() (
(![]() 是非负整数,
是非负整数,![]() 是正整数,且
是正整数,且![]() ,
,![]() 互质),利用反证法可得结论.
互质),利用反证法可得结论.
试题解析:(1)![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,
,
所以![]() .
.
(2)![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]() ,所以
,所以![]() ,
,
解![]() 得(
得(![]() ,舍去).
,舍去).
②当![]() ,即
,即![]() 时,
时,![]() ,所以
,所以![]() ,
,
解![]() (
(![]() ,舍去).
,舍去).
③当![]() ,即
,即![]() 时,
时,![]() ,所以
,所以![]() ,
,
解得![]() (
(![]() 舍去).
舍去).
综上![]() .
.
(2)成立.由![]() 是有理数,可知对一切正整数
是有理数,可知对一切正整数![]() ,
,![]() 为0或正有理数,
为0或正有理数,
可设![]() (
(![]() 是非负整数,
是非负整数,![]() 是正整数,且
是正整数,且![]() 既约).
既约).
①由![]() ,可得
,可得![]() ;
;
②若![]() ,设
,设![]() (
(![]() ,
,![]() ,
,![]() 是非负整数),
是非负整数),
则![]() ,而由
,而由![]() 得
得![]() ,
,
![]() ,故
,故![]() ,
,![]() ,可得
,可得![]() .
.
若![]() 则
则![]() ,
,
若![]() 均不为0,则这
均不为0,则这![]() 正整数互不相同且都小于
正整数互不相同且都小于![]() ,
,
但小于![]() 的正整数共有
的正整数共有![]() 个,矛盾.
个,矛盾.
故![]() 中至少有一个为0,即存在
中至少有一个为0,即存在![]() ,使得
,使得![]() .
.
从而数列![]() 中
中![]() 以及它之后的项均为0,所以对不大于
以及它之后的项均为0,所以对不大于![]() 的自然数
的自然数![]() ,都有
,都有![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目