题目内容
11. 在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为DD1和BB1的中点.
在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为DD1和BB1的中点.(1)求证:四边形AEC1F为平行四边形;
(2)求直线AA1与平面AEC1F所成角的正弦值.
分析 (1)取CC1的中点H,连接BH,EH,运用平行四边形的判定和性质,即可得证;
(2)设A1到平面AEC1F的距离为d,运用等积法,可得${V}_{{A}_{1}-AEF}$=${V}_{F-{A}_{1}AE}$,运用三棱锥的体积公式,计算即可得到所求值.
解答 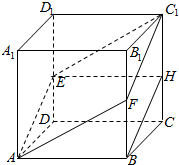 解:(1)取CC1的中点H,连接BH,EH,
解:(1)取CC1的中点H,连接BH,EH,
在正方形BCC1B1中,BF∥HC1,BF=HC1,可得BFC1H为平行四边形,
即有BH∥FC1,BH=FC1,
又AB∥EH,AB=EH,可得四边形ABHE为平行四边形,
即有AE∥BH,AE=BH,
则AE=FC1,AE∥FC1,可得四边形AEC1F为平行四边形;
(2)设A1到平面AEC1F的距离为d,
直线AA1与平面AEC1F所成角θ的正弦值为$\frac{d}{a}$,
由${V}_{{A}_{1}-AEF}$=${V}_{F-{A}_{1}AE}$,可得$\frac{1}{3}$d•S△AEF=$\frac{1}{3}$a•${S}_{△{A}_{1}AE}$,
即为d•$\frac{1}{2}$${S}_{菱形AE{C}_{1}F}$=a•$\frac{1}{2}$a2,即有d=$\frac{{a}^{3}}{\frac{1}{2}\sqrt{2}a•\sqrt{3}a}$=$\frac{\sqrt{6}}{3}$a,
即有直线AA1与平面AEC1F所成角的正弦值为$\frac{\sqrt{6}}{3}$.
点评 本题考查空间线线的位置关系的判断和线面角的求法,注意运用平行四边形的判定和性质,以及体积转换法,考查运算能力,属于中档题.

练习册系列答案
相关题目
1.已知直线的斜截式方程是y=$\sqrt{3}$x+1,则此直线的倾斜角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
19.已知函数f(x)=cos$\frac{2π}{3}cos(\frac{π}{2}+2x)$,则函数f(x)满足( )
| A. | f(x)的最小正周期是2π | B. | 当x∈$[-\frac{π}{6},\frac{π}{3}]$时,f(x)的值域为$[-\frac{{\sqrt{3}}}{4},\frac{{\sqrt{3}}}{4}]$ | ||
| C. | f(x)的图象关于直线x=$\frac{3π}{4}$对称 | D. | 若x1≠x2,则f(x1)≠f(x2) |
6.已知集A={x|1<x<2},B={x|x<a},满足A?B,则( )
| A. | a≥2 | B. | a≤1 | C. | a≥1 | D. | a≤2 |
16.直线x-y+6=0被圆(x+2)2+y2=16截得的弦长等于( )
| A. | $2\sqrt{2}$ | B. | $3\sqrt{2}$ | C. | $4\sqrt{2}$ | D. | $12\sqrt{2}$ |