题目内容
设函数f(x)=ax2+8x+3(a<0),对于给定的负数a,有一个 最大正数l(a),使得在整个区间[0,l(a)]上,不等式|f(x)|≤5都成立。问:a为何值时l(a)最大?求出这个最大的l(a)并证明你的结论.
最大正数l(a),使得在整个区间[0,l(a)]上,不等式|f(x)|≤5都成立。问:a为何值时l(a)最大?求出这个最大的l(a)并证明你的结论.
f(x)= =a(x+
=a(x+ )2+3-
)2+3- .故抛物线的顶点为
.故抛物线的顶点为
即x=- 时,f(x)max =3-
时,f(x)max =3- .
.
(1)当3- >5,即-8<a<0时,l(a)是方程ax2+8x+3=5的较小根,故l(a)=
>5,即-8<a<0时,l(a)是方程ax2+8x+3=5的较小根,故l(a)=



练习册系列答案
相关题目
抽样统计甲、乙两位射击运动员的 5次训练成绩(单位:环),结果如下:
5次训练成绩(单位:环),结果如下:
| 运动员 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 甲 | 87 | 91 | 90 | 89 | 93 |
| 乙 | 89 | 90 | 91 | 88 | 92 |
则成绩较为稳定(方差较小)的那位运动员成绩的方差为________.
 ,B=
,B= ,则A∩∁RB=________.
,则A∩∁RB=________. ,函数
,函数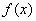 满足
满足 ,若
,若 ,则
,则 .
. 是给定的常数,
是给定的常数,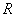 上的奇函数,且在
上的奇函数,且在 上是增函数,
上是增函数, ,
, ,则t的取值范围是________.
,则t的取值范围是________. 的解”有如下解题思路:设
的解”有如下解题思路:设 ,则
,则 在R上单调递减,且
在R上单调递减,且 ,所以原方程有唯一解
,所以原方程有唯一解 。类比上述解题思路,不等式
。类比上述解题思路,不等式 的解集为________.
的解集为________. ,它的一个焦点坐标是
,它的一个焦点坐标是 ,则双曲线方程是___.
,则双曲线方程是___.