题目内容
12．在△ABC中，AB=3，BC=4，∠B=90°．以AC所在直线为轴，其余各边旋转一周形成的曲面围成一个几何体，则该几何体的体积为（ ）| A． | 12π | B． | 16π | C． | $\frac{48π}{5}$ | D． | $\frac{144π}{5}$ |
分析 旋转体为两个同底的圆锥的组合体，求出底面半径和高即可求出体积．
解答 解：AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5，∴△ABC的斜边AC上的高为$\frac{3×4}{5}$=$\frac{12}{5}$．
则旋转而成的几何体为两个同底的圆锥的组合体，它们的底面半径为$\frac{12}{5}$，它们的高度之和为5．
∴几何体的体积V=$\frac{1}{3}×$π×（$\frac{12}{5}$）2×5=$\frac{48π}{5}$．
故选：C．
点评 本题考查了旋转体的结构特征和体积计算，属于基础题．
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
2．若函数f（x）=log2（3x+1）+$\frac{a}{lo{g}_{2}（{3}^{x}+1）}$在[1，+∞）上无零点，则实数a的取值范围是（ ）
| A． | （-4，2） | B． | （-2，4） | C． | （0，+∞） | D． | （-4，+∞） |
20．已知两点A（4，0），B（0，5），点C圆x2+y2=9上的任意一点，则△ABC面积的最小值是（ ）
| A． | 10-$\frac{3\sqrt{41}}{2}$ | B． | 10+$\frac{3\sqrt{41}}{2}$ | C． | 10-$\frac{\sqrt{41}}{2}$ | D． | 10+$\frac{\sqrt{41}}{2}$ |
7．
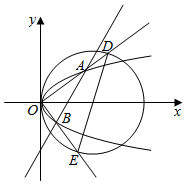如图所示，过点（1，0）的直线与抛物线y2=x交于A、B两点，射线OA和OB分别和圆（x-2）2+y2=4交于D、E两点，若$\frac{{S}_{△OAB}}{{S}_{△ODE}}$=λ，则λ的最小值是（ ）
如图所示，过点（1，0）的直线与抛物线y2=x交于A、B两点，射线OA和OB分别和圆（x-2）2+y2=4交于D、E两点，若$\frac{{S}_{△OAB}}{{S}_{△ODE}}$=λ，则λ的最小值是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
17．圆锥的底面半径为2，高为$\sqrt{5}$，则圆锥的侧面积为（ ）
| A． | 3π | B． | 12π | C． | 5π | D． | 6π |
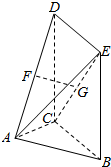如图，平面DCBE⊥平面ABC，四边形DCBE为矩形，且BC=$\sqrt{2}$AB=$\sqrt{2}$AC，F、G分别为AD、CE的中点．
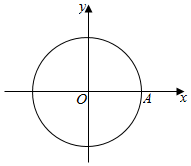如图，圆周上点A依逆时针方向做匀速圆周运动，已知A点1分钟转过θ（0°＜θ＜180°），2分钟到第三象限，16分钟后回到原来的位置，求θ．