题目内容
已知f(x)=cos(ωx+φ) 的最小正周期为π,且f
的最小正周期为π,且f =
= .
.
(1)求ω和φ的值;
(2)在给定坐标系中作出函数f(x)在[0,π]上的图象;

(3)若f(x)> ,求x的取值范围.
,求x的取值范围.
 的最小正周期为π,且f
的最小正周期为π,且f =
= .
.(1)求ω和φ的值;
(2)在给定坐标系中作出函数f(x)在[0,π]上的图象;

(3)若f(x)>
 ,求x的取值范围.
,求x的取值范围.(1)ω=2φ=- .(2)
.(2)

(3)
 .(2)
.(2)
(3)

(1)周期T= =π,∴ω=2,
=π,∴ω=2,
∵f =cos
=cos =cos
=cos =-sinφ=
=-sinφ= ,-
,- <φ<0,∴φ=-
<φ<0,∴φ=- .
.
(2)f(x)=cos ,列表如下:
,列表如下:
图象如图:

(3)∵cos >
> ,∴2kπ-
,∴2kπ- <2x-
<2x- <2kπ+
<2kπ+ ,
,
∴2kπ+ <2x<2kπ+
<2x<2kπ+ ,∴kπ+
,∴kπ+ <x<kπ+
<x<kπ+ ,k∈Z,
,k∈Z,
∴x的取值范围是 .
.
 =π,∴ω=2,
=π,∴ω=2,∵f
 =cos
=cos =cos
=cos =-sinφ=
=-sinφ= ,-
,- <φ<0,∴φ=-
<φ<0,∴φ=- .
.(2)f(x)=cos
 ,列表如下:
,列表如下:2x- | - | 0 |  | π |  π π |  π π |
| x | 0 |  |  π π |  π π |  π π | π |
| f(x) |  | 1 | 0 | -1 | 0 |  |

(3)∵cos
 >
> ,∴2kπ-
,∴2kπ- <2x-
<2x- <2kπ+
<2kπ+ ,
,∴2kπ+
 <2x<2kπ+
<2x<2kπ+ ,∴kπ+
,∴kπ+ <x<kπ+
<x<kπ+ ,k∈Z,
,k∈Z,∴x的取值范围是
 .
.
练习册系列答案
相关题目

 取得最小值时θ的值.
取得最小值时θ的值.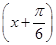 ,其中x∈
,其中x∈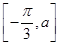 ,若f(x)的值域是
,若f(x)的值域是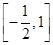 ,则a的取值范围是________.
,则a的取值范围是________.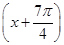 +cos
+cos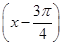 ,x∈R.
,x∈R.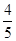 ,cos(β+α)=-
,cos(β+α)=-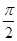 ,求证:[f(β)]2-2=0.
,求证:[f(β)]2-2=0.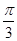 ,则f
,则f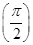 =________.
=________.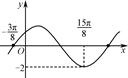
 在
在 上单调递减,则
上单调递减,则 可以是( )
可以是( )


 ,直线x=
,直线x= 是其图象的一条对称轴,则符合条件的解析式为( )
是其图象的一条对称轴,则符合条件的解析式为( )

 +2
+2 )的一个单调区间是 ( )
)的一个单调区间是 ( ) ]
] ,
, ]
] ]
]