题目内容
已知: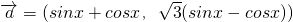 ,
,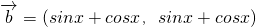 ,函数
,函数
(I)把f(x)化为Asin(?x+φ)+b的形式;
(II)求f(x)的最小正周期和单调递增区间;
(Ⅲ)若f(α)=f(β),且α与β的终边不共线,求sin(α+β)的值.
解:(Ⅰ)由题意可得:

= …(4分)
…(4分)
(Ⅱ)T=π…(5分)
由正弦函数的单调区间可得: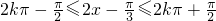
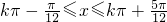
所以单调递增区间为 .…(7分)
.…(7分)
(Ⅲ)由
得: 或
或 …(8分)
…(8分)
所以α-β=kπ或 ,k∈Z
,k∈Z
因为α与β的终边不共线,所以
当k为偶数时, ;当k为奇数时,
;当k为奇数时, .…(10分)
.…(10分)
分析:(Ⅰ)由题意可得根据两角差得正弦该生可得 .
.
(Ⅱ)由(I)可得结合正弦函数的周期性与单调区间可得函数的周期与单调区间.
(Ⅲ)由题意可得:α-β=kπ或 ,k∈Z,由α与β的终边不共线,可得
,k∈Z,由α与β的终边不共线,可得 ,金额得到答案.
,金额得到答案.
点评:解决此类问题的关键是熟练掌握正弦函数的有关性质,以及平面向量的数量积运算.

=
 …(4分)
…(4分)(Ⅱ)T=π…(5分)
由正弦函数的单调区间可得:
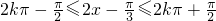
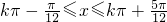
所以单调递增区间为
 .…(7分)
.…(7分)(Ⅲ)由

得:
 或
或 …(8分)
…(8分)所以α-β=kπ或
 ,k∈Z
,k∈Z因为α与β的终边不共线,所以

当k为偶数时,
 ;当k为奇数时,
;当k为奇数时, .…(10分)
.…(10分)分析:(Ⅰ)由题意可得根据两角差得正弦该生可得
 .
.(Ⅱ)由(I)可得结合正弦函数的周期性与单调区间可得函数的周期与单调区间.
(Ⅲ)由题意可得:α-β=kπ或
 ,k∈Z,由α与β的终边不共线,可得
,k∈Z,由α与β的终边不共线,可得 ,金额得到答案.
,金额得到答案.点评:解决此类问题的关键是熟练掌握正弦函数的有关性质,以及平面向量的数量积运算.

练习册系列答案
相关题目
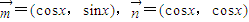 ,设函数
,设函数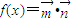
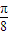 个单位得到的,求g(x)的最大值及使g(x)取得最大值时x的值.
个单位得到的,求g(x)的最大值及使g(x)取得最大值时x的值. ,
,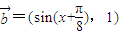 ,函数
,函数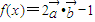
 图象的对称中心坐标与对称轴方程和单调递增区间.
图象的对称中心坐标与对称轴方程和单调递增区间.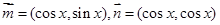 ,设函数
,设函数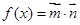
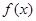 的解析式,并求最小正周期;
的解析式,并求最小正周期;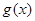 的图像是由函数
的图像是由函数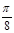 个单位得到的,求
个单位得到的,求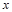 的值.
的值. 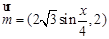 ,
,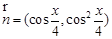 .函数
.函数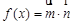 .
.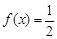 ,求
,求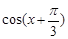 的值;
的值;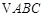 中,角
中,角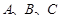 的对边分别是
的对边分别是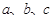 ,且满足
,且满足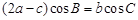 ,
,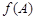 的取值范围.
的取值范围.