题目内容
已知向量 ,
,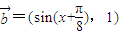 ,函数
,函数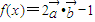
(I)求函数f(x)的解析式,并求其最小正周期;
(II)求函数
 图象的对称中心坐标与对称轴方程和单调递增区间.
图象的对称中心坐标与对称轴方程和单调递增区间.
【答案】分析:(I)利用两个向量的数量积公式与两角和的三角公式化简函数f(x)的解析式,求出周期.
(II)利用弦函数的对称中心、对称轴的定义求得对称中心坐标与对称轴方程,由 ,求得x的范围,即得函数
,求得x的范围,即得函数 的增区间.
的增区间.
解答:解:(I) =
=
= ,∴
,∴ .
.
(II)∵ =
= ,令y=0即
,令y=0即 得 x=kπ,
得 x=kπ,
∴对称点(kπ,0)k∈Z,由 得
得  ,
,
∴对称轴方程为 .
.
∵ =
= 的单调增区间∴sinx递减,∴
的单调增区间∴sinx递减,∴ ,
,
∴ 的单调递增区间是
的单调递增区间是 .
.
点评:本题考查三角函数中的恒等变换,正弦函数的单调区间和周期性,由 ,求得函数
,求得函数 的增区间,是解题的难点.
的增区间,是解题的难点.
(II)利用弦函数的对称中心、对称轴的定义求得对称中心坐标与对称轴方程,由
 ,求得x的范围,即得函数
,求得x的范围,即得函数 的增区间.
的增区间.解答:解:(I)
 =
=
=
 ,∴
,∴ .
.(II)∵
 =
= ,令y=0即
,令y=0即 得 x=kπ,
得 x=kπ,∴对称点(kπ,0)k∈Z,由
 得
得  ,
,∴对称轴方程为
 .
.∵
 =
= 的单调增区间∴sinx递减,∴
的单调增区间∴sinx递减,∴ ,
,∴
 的单调递增区间是
的单调递增区间是 .
.点评:本题考查三角函数中的恒等变换,正弦函数的单调区间和周期性,由
 ,求得函数
,求得函数 的增区间,是解题的难点.
的增区间,是解题的难点. 
练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
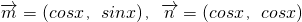 ,设函数
,设函数
 个单位得到的,求g(x)的最大值及使g(x)取得最大值时x的值.
个单位得到的,求g(x)的最大值及使g(x)取得最大值时x的值.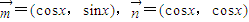 ,设函数
,设函数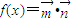
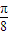 个单位得到的,求g(x)的最大值及使g(x)取得最大值时x的值.
个单位得到的,求g(x)的最大值及使g(x)取得最大值时x的值.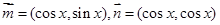 ,设函数
,设函数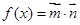
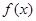 的解析式,并求最小正周期;
的解析式,并求最小正周期;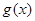 的图像是由函数
的图像是由函数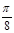 个单位得到的,求
个单位得到的,求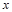 的值.
的值.  ,定义函数
,定义函数
 最小正周期;
最小正周期; ,求边AC的长.
,求边AC的长.