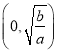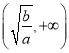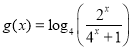题目内容

【题目】已知集合A＝{x|0}，B＝{x|x2﹣3x+2＜0}，U＝R，求

（1）A∩B；

（2）A∪B；

（3）（UA）∩B．

【答案】（1）x|1＜x}；（2）{x|﹣5＜x＜2}；（3）{x|x≤﹣5或x}∩{x|1＜x＜2}＝{x|x＜2}．

【解析】

分别计算集合再求解即可.

集合A＝{x|0}＝{x|﹣5＜x}，

B＝{x|x2﹣3x+2＜0}＝{x|1＜x＜2}，U＝R，

（1）A∩B＝{x|﹣5＜x}∩{x|1＜x＜2}＝{x|1＜x}；

（2）A∪B＝{x|﹣5＜x}∪{x|1＜x＜2}＝{x|﹣5＜x＜2}；

（3）∵UA＝{x|x≤﹣5或x}，

∴（UA）∩B＝{x|x≤﹣5或x}∩{x|1＜x＜2}＝{x|x＜2}．

练习册系列答案
相关题目

【题目】已知向量， .

（1）若分别表示将一枚质地均匀的正方体骰子（六个面的点数分别为1,2,3,4,5,6），先后抛掷两次时第一次、第二次出现的点数，求满足的概率；

（2）若在连续区间上取值，求满足的概率.

【题目】已知椭圆：，其左、右焦点分别为，上顶点为，为坐标原点，过的直线交椭圆于两点，.

（1）若直线垂直于轴，求的值；

（2）若，直线的斜率为，则椭圆上是否存在一点，使得关于直线成轴对称？如果存在，求出点的坐标；如果不存在，请说明理由；

（3）设直线:上总存在点满足，当的取值最小时，求直线的倾斜角.

【题目】已知二次函数满足①对于任意，都有；②；③的图像与轴的两个交点之间的距离为4.

（1）求的解析式；

（2）记

①若为单调函数，求的取值范围；

②记的最小值为，讨论函数零点的个数.

【题目】已知函数具有以下性质：在上是减函数，在上是增函数.

（1）若在上是增函数，求实数的取值范围；

（2）若，，求的值域和单调区间.

【题目】如图，直三棱柱中，且，，分别为，的中点.

（1）证明：平面；

（2）若直线与平面所成的角的大小为，求锐二面角的正切值.

【题目】对于定义在上的函数，若存在距离为的两条直线和，使得对任意都有恒成立，则称函数有一个宽度为的通道．给出下列函数：

①； ②； ③； ④．

其中在区间上有一个通道宽度为的函数是__________（写出所有正确的序号）．

【题目】已知函数（，，为自然对数的底数），若对于恒成立．

（1）求实数的值；

（2）证明：存在唯一极大值点，且．

【题目】为了解七班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：

喜爱打篮球

不喜爱打篮球

合

男生

5

女生

10

合计

50

已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为．

（1）请将上面的列联表补充完整(不用写计算过程)；

（2）能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关？说明你的理由；

（3）现从女生中抽取2人进一步调查，设其中喜爱打篮球的女生人数为，求的分布列与期望.

下面的临界值表供参考：

0.15

0.10

0.05[

0.025

0.01

0.005

0.001

2.072

2.70

3.841

5.024

6.635

7.879

10.82

(参考公式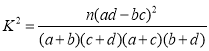：，其中)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网