题目内容
10.在三棱锥P-ABC中,PA,PB,PC两两互相垂直,且AB=4,AC=5,则BC的取值范围是(3,$\sqrt{41}$).分析 如图设PA、PB、PC的长分别为a、b、c,BC=m.由PA,PB,PC两两互相垂直,得a2+b2=16,a2+c2=25,
b2+c2=m2⇒m2=41-2a2,且a2<16,a2<25⇒-2a2>-32,⇒-2a2>-50⇒⇒-2a2>-32⇒m2=41-2a2>9
在△ABC中,$\left\{\begin{array}{l}{m<5+4}\\{4<5+m}\\{5<4+m}\end{array}\right.$⇒3<m<$\sqrt{41}$.
解答 解:如图设PA、PB、PC的长分别为a、b、c,BC=m.∵PA,PB,PC两两互相垂直,
∴a2+b2=16,a2+c2=25,b2+c2=m2⇒m2=41-2a2,
且a2<16,a2<25⇒-2a2>-32,⇒-2a2>-50⇒⇒-2a2>-32⇒m2=41-2a2>9
⇒m>3
在△ABC中,$\left\{\begin{array}{l}{m<5+4}\\{4<5+m}\\{5<4+m}\end{array}\right.$⇒3<m<$\sqrt{41}$
故答案为(3,$\sqrt{41}$)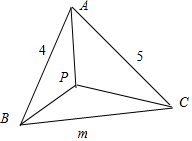
点评 本题考查了空间位置关系,关键是把空间问题转化为平面问题,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.若函数f(x)=a(x-2)ex+lnx+$\frac{1}{x}$存在唯一的极值点,且此极值大于0,则( )
| A. | 0≤a<$\frac{1}{e}$ | B. | 0≤a<$\frac{1}{{e}^{2}}$ | C. | -$\frac{1}{e}$<a<$\frac{1}{{e}^{2}}$ | D. | 0≤a<$\frac{1}{e}$或a=-$\frac{1}{e}$ |
19.设复数z满足z+i=i(2-i),则$\overline{z}$=( )
| A. | 1+3i | B. | -1+3i | C. | 1-i | D. | -1+i |
 如图,在三棱柱ABC-A1B1C1中,AB⊥平面BCC1B1,$∠BC{C_1}=\frac{π}{3},AB=B{B_1}=2,BC=1,D$为CC1的中点.
如图,在三棱柱ABC-A1B1C1中,AB⊥平面BCC1B1,$∠BC{C_1}=\frac{π}{3},AB=B{B_1}=2,BC=1,D$为CC1的中点.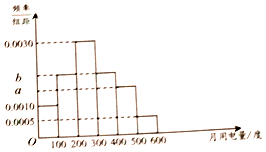 某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.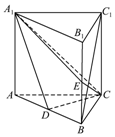 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=2,AB=2$\sqrt{2}$.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=2,AB=2$\sqrt{2}$.