题目内容
20.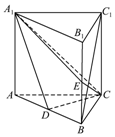 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=2,AB=2$\sqrt{2}$.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=2,AB=2$\sqrt{2}$.(Ⅰ)证明:BC1∥平面A1CD;
(Ⅱ)求锐二面角D-A1C-E的余弦值.
分析 (Ⅰ)连结AC1,交A1C于点O,连结DO,证明OD∥BC1,然后证明BC1∥平面A1CD.
(Ⅱ)由以C为坐标原点,$\overrightarrow{CA}$方向为x轴正方向,$\overrightarrow{CB}$方向为y轴正方向,$\overrightarrow{C{C_1}}$方向为z轴正方向,建立空间直角坐标系Cxyz,求出相关点的坐标,平面A1CD的法向量,平面A1CE的法向量,利用空间向量的数量积求解即可.
解答 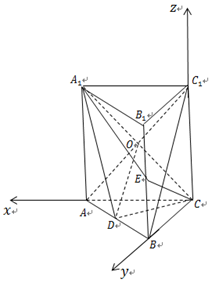 解:(Ⅰ)连结AC1,交A1C于点O,连结DO,则O为AC1的中点,因为D为AB的中点,所以OD∥BC1,又因为OD?平面A1CD,BC1?平面A1CD,∴BC1∥平面A1CD…(4分)
解:(Ⅰ)连结AC1,交A1C于点O,连结DO,则O为AC1的中点,因为D为AB的中点,所以OD∥BC1,又因为OD?平面A1CD,BC1?平面A1CD,∴BC1∥平面A1CD…(4分)
(Ⅱ)由$A{A_1}=AC=CB=2,AB=2\sqrt{2}$,可知AC⊥BC,以C为坐标原点,$\overrightarrow{CA}$方向为x轴正方向,$\overrightarrow{CB}$方向为y轴正方向,$\overrightarrow{C{C_1}}$方向为z轴正方向,建立空间直角坐标系Cxyz,
则D(1,1,0),E(0,2,1),A1(2,0,2),$\overrightarrow{CD}=({1,1,0})$,$\overrightarrow{CE}=({0,2,1})$,$\overrightarrow{C{A_1}}=({2,0,2})$
设$\overrightarrow n=({x,y,z})$是平面A1CD的法向量,则$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{CD}=0\\ \overrightarrow n•\overrightarrow{C{A_1}}=0\end{array}\right.$即$\left\{\begin{array}{l}x+y=0\\ 2x+2z=0\end{array}\right.$
可取$\overrightarrow n=({1,-1,-1})$.…(6分)
同理,设$\overrightarrow m$是平面A1CE的法向量,则$\left\{\begin{array}{l}\overrightarrow m•\overrightarrow{CE}=0\\ \overrightarrow m•\overrightarrow{C{A_1}}=0\end{array}\right.$,
可取$\overrightarrow m=({2,1,-2})$.…(8分)
从而$cos?\overrightarrow n,\overrightarrow m>=\frac{\overrightarrow n•\overrightarrow m}{{|{\overrightarrow n}||{\overrightarrow m}|}}=\frac{{\sqrt{3}}}{3}$…(10分)
所以锐二面角D-A1C-E的余弦值为$\frac{{\sqrt{3}}}{3}$…(12分)
点评 本题考查空间向量的数量积的应用,二面角的平面角的求法,直线与平面平行的判定定理的应用,考查计算能力.

| A. | 10 | B. | 20 | C. | 25 | D. | 35 |
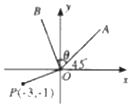 如图,已知点P(-3,-1),OA为第一象限的角平分线,将OA沿逆时针旋转θ角到OB,若$\overrightarrow{OP}•\overrightarrow{OB}=0$,则tanθ的值为( )
如图,已知点P(-3,-1),OA为第一象限的角平分线,将OA沿逆时针旋转θ角到OB,若$\overrightarrow{OP}•\overrightarrow{OB}=0$,则tanθ的值为( )| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
| A. | f2(f(0))=f(f2(0))?? | B. | f2(f(1))=f(f2(1))?? | C. | f2(f(2))=f(f2(2))?? | D. | f2(f(3))=f(f2(3))?? |
| A. | 672 | B. | 673 | C. | 1342 | D. | 1344 |
| A. | 函数y=f(x)•g(x)的周期为2 | |
| B. | 函数y=f(x)•g(x)的最大值为1 | |
| C. | 将f(x)的图象向左平移$\frac{π}{2}$个单位后得到g(x)的图象 | |
| D. | 将f(x)的图象向右平移$\frac{π}{2}$个单位后得到g(x)的图象 |