题目内容
设平面上3个向量 的模均为1,它们相互之间的夹角为120°.
的模均为1,它们相互之间的夹角为120°.
(1)判断 与
与 是否垂直?并说明理由.
是否垂直?并说明理由.
(2)若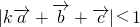 ,(k∈R),求k的取值范围.
,(k∈R),求k的取值范围.
解:(1)∵ ,
, =1×1cos120°-1×1cos120°=0,
=1×1cos120°-1×1cos120°=0,
∴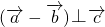 .
.
(2)∵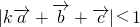 ,∴
,∴ ,
,
∴ ,
,
∴k2-2k<0,∴k∈(0,2).
分析:(1)利用两个向量的数量积的定义,计算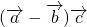 的值等于0,可得
的值等于0,可得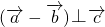 .
.
(2)由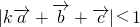 可得
可得  ,化简可得k2-2k<0,解不等式求得k的取值范围.
,化简可得k2-2k<0,解不等式求得k的取值范围.
点评:本题考查两个向量的数量积的定义,两个向量垂直的条件,由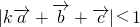 得到
得到 ,是解题
,是解题
的关键.
 ,
, =1×1cos120°-1×1cos120°=0,
=1×1cos120°-1×1cos120°=0,∴
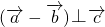 .
.(2)∵
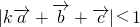 ,∴
,∴ ,
,∴
 ,
,∴k2-2k<0,∴k∈(0,2).
分析:(1)利用两个向量的数量积的定义,计算
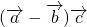 的值等于0,可得
的值等于0,可得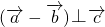 .
.(2)由
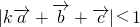 可得
可得  ,化简可得k2-2k<0,解不等式求得k的取值范围.
,化简可得k2-2k<0,解不等式求得k的取值范围.点评:本题考查两个向量的数量积的定义,两个向量垂直的条件,由
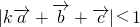 得到
得到 ,是解题
,是解题的关键.

练习册系列答案
相关题目
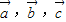 的模均为1,它们相互之间的夹角为120°.
的模均为1,它们相互之间的夹角为120°.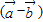 与
与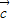 是否垂直?并说明理由.
是否垂直?并说明理由.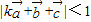 ,(k∈R),求k的取值范围.
,(k∈R),求k的取值范围.