题目内容

12．设某种机械设备能够连续正常工作10000小时的概率为0.85，能够连续正常工作15000小时的概率为0.75，现有一台连续工作10000小时的这种机械，它能够连续正常工作15000小时的概率是$\frac{15}{17}$．

分析 设“某种机械设备能够连续正常工作10000小时”为事件A，“某种机械设备能够连续正常工作15000小时”为事件B，则P（A）=0.85，P（AB）=0.75，由此利用条件概率能求出现有一台连续工作10000小时的这种机械，它能够连续正常工作15000小时的概率．

解答 解：设“某种机械设备能够连续正常工作10000小时”为事件A，
“某种机械设备能够连续正常工作15000小时”为事件B，
P（A）=0.85，P（AB）=0.75，
现有一台连续工作10000小时的这种机械，
它能够连续正常工作15000小时的概率：
P（B/A）=$\frac{P（AB）}{P（A）}$=$\frac{0.75}{0.85}$=$\frac{15}{17}$．
故答案为：$\frac{15}{17}$．

点评 本题考查概率的求法，考查条件概率等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．

练习册系列答案
相关题目
2．求证：函数f（x）=$\left\{\begin{array}{l}{x（2-x），（x≥0）}\\{-x（2+x），（x＜0）}\end{array}\right.$是偶函数．
3．已知直线l⊥平面α，直线m∥平面β，则下列命题正确的是（　　）
A．若α⊥β，则l∥mB．若α∥β，则l⊥mC．若l∥β，则m⊥αD．若l⊥m，则α∥β
20．已知函数f（x）=|x+$\frac{4}{m}$|+|x-m|，（m＞0）．
（1）若函数f（x）的最小值为5，求实数m的值；
（2）求使得不等式f（1）＞5成立的实数m的取值范围．
7．设随机变量ξ服从正态分布N（2，4）若P（ξ＜a-3）=p（ξ＞2a+1），则实数a的值是（　　）
A．-4B．$\frac{4}{3}$C．2D．$\frac{10}{3}$
17．已知数列{an}的首项a1=1，且an+1=2an+1（n∈N*）
（Ⅰ）证明数列{an+1}是等比数列，并求数列{an}的通项公式；
（Ⅱ）设bn=$\frac{n}{{a}_{n}+1}$，求数列{bn}的前n项和Sn；
（Ⅲ）在条件（Ⅱ）下对任意正整数n，不等式Sn+$\frac{n+1}{{2}^{n}}$-1＞（-1）n•a恒成立，求实数a的取值范围．
4．已知$\overrightarrow{a}$=（2，x-3），$\overrightarrow{b}$=（x，2），则“x=-1”是“$\overrightarrow{a}$∥$\overrightarrow{b}$”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
13．在△ABC中，角A，B，C所对应的边分别为a，b，c，已知B=$\frac{π}{4}$，cosA-cos2A=0
（1）求角C；  
（2）若b2+c2=a-bc+2，求a，c值．
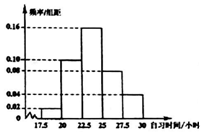14．某校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是[17.5，30]，样本数据分组为[17.5，20），[17.5，20），[20，22.5），[22.5，25），[25，27.5），[27.5，30]．根据直方图，这200名学生中每周的自习时间不少于24小时的人数是（　　）
A．76B．92C．108D．114

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网