题目内容
(本小题满分12分)设数列 的前
的前 项和为
项和为 ,已知
,已知 ,
, (
(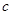 为常数,
为常数, ),且
),且 成等差数列.
成等差数列.
(1) 求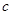 的值;
的值;
(2) 求数列 的通项公式;
的通项公式;
(3) 若数列 是首项为1,公比为
是首项为1,公比为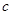 的等比数列,记
的等比数列,记


.求证: ,(
,( ).
).
(1)  ;(2)
;(2)  ; (3)求出
; (3)求出 的值,然后证明
的值,然后证明 。
。
解析试题分析:(1)∵ ,
, ,∴
,∴ ,
,
∴ .
.
∵ 成等差数列,∴
成等差数列,∴ ,即
,即 ,∴
,∴ .
.
解得 ,或
,或 (舍去).…………4分
(舍去).…………4分
(2)∵ ,
, ,∴
,∴ ,
,
∴ ,
,
又 ,∴数列
,∴数列 的通项公式是
的通项公式是 .…………7分
.…………7分
(3)证明:∵数列 是首项为1,公比为
是首项为1,公比为 的等比数列,∴
的等比数列,∴ .
.
又 ,所以
,所以 ①
① ②
②
将①乘以2得:  ③
③
①-③得:  ,
,
整理得: 
将②乘以 得:
得:  ④
④
②-④整理得: 
∴ 
 …………12
…………12
考点:等差数列的性质;等差数列的前n项和;等比数列的通项公式;等比数列的前n项和.
点评:此题考查了等差数列的性质,等差数列的前n项和公式,等比数列的通项公式,以及等比数列的前n项和公式,熟练掌握公式及性质是解本题的关键.本题也充分考查了学生的分析问题、解决问题的能力。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 }满足
}满足 ,且
,且
 }是等差数列;
}是等差数列;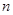 项之和
项之和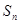 ,求证:
,求证: .
. }的前n项和为
}的前n项和为 ,已知
,已知 ,
, .
.
 ,求数列{
,求数列{ }的前项和
}的前项和 .
. 中的
中的 、
、 、
、 .
. .
. 是公差不为0的等差数列
是公差不为0的等差数列 的前n项和,且
的前n项和,且 成等比数列。
成等比数列。 ,求
,求 ,
, 是数列
是数列 的前n项和,求使得
的前n项和,求使得 对所有
对所有 都成立的最小正整数
都成立的最小正整数 。
。 中的数按上小下大、左小右大的原则排成如下三角形数表:
中的数按上小下大、左小右大的原则排成如下三角形数表:
 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行、从左往右数第
行、从左往右数第 个数.
个数. ,求
,求 的值;
的值; ,求证
,求证 .(本题满分14分)
.(本题满分14分) 的公差大于0,且
的公差大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前
的前 项的和为
项的和为 ,且
,且 .
. ,求证:
,求证: ;
; 的前
的前 .
. 是公差不为零的等差数列,
是公差不为零的等差数列,  成等比数列.
成等比数列. 的前n项和
的前n项和