题目内容
(本小题满分15分)
若S 是公差不为0的等差数列
是公差不为0的等差数列 的前n项和,且
的前n项和,且 成等比数列。
成等比数列。
(1)求等比数列 的公比;
的公比;
(2)若 ,求
,求 的通项公式;
的通项公式;
(3)在(2)的条件下,设 ,
, 是数列
是数列 的前n项和,求使得
的前n项和,求使得 对所有
对所有 都成立的最小正整数
都成立的最小正整数 。
。
(1)4;(2) ;(3)30.
;(3)30.
解析试题分析:∵数列{an}为等差数列,∴ ,
,
∵S1,S2,S4成等比数列, ∴ S1·S4 =S22
∴  ,∴
,∴
∵公差d不等于0,∴ ---------2分
---------2分
(1) -------------4分
-------------4分
(2)∵S2 =4,∴ ,又
,又 ,
,
∴ , ∴
, ∴ 。 ----------8分
。 ----------8分
(3)∵ -------9分
-------9分
∴ …
…
 ----11分
----11分
要使 对所有
对所有 恒成立,∴
恒成立,∴ ,
, , ---------13分
, ---------13分
∵ , ∴
, ∴ 的最小值为30。 ---------14分
的最小值为30。 ---------14分
考点:等比数列的性质;等差数列的性质;通项公式的求法;前n项和的求法。
点评:常见的裂项公式: ,
, ,
, ,
, ,
, ,
,

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 满足
满足 ,
, ;数列
;数列 满足
满足 ,
,  .
. 和
和 的通项公式;
的通项公式; 、
、 的前
的前 项和
项和 ,
, .
.
 的最小值.
的最小值. 的前
的前 项和为
项和为 ,前
,前 项和为
项和为 .
.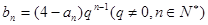 , 求数列
, 求数列 的前
的前 项和
项和 .
. 中,
中, ,其前
,其前 项和为
项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数, ,公比为
,公比为 ,且
,且 ,
,  .
. 与
与 ;
; .
. 的前
的前 项和为
项和为 ,已知
,已知 ,
, (
(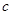 为常数,
为常数, ),且
),且 成等差数列.
成等差数列. 是首项为1,公比为
是首项为1,公比为


 ,(
,( 中,已知
中,已知 。(1)求数列
。(1)求数列 是等差数列,且
是等差数列,且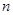 项和
项和 ,求
,求 bn=1.
bn=1. ;
; 的前
的前 项和为
项和为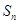 ,若
,若 ,且
,且 成等比数列.
成等比数列. 的前
的前 ,求证
,求证 .
.