题目内容
1.已知集合A={x|2≤2x≤16},B={x|log${\;}_{\frac{1}{3}}$x<-1}.(1)求A∩B,∁RB∪A;
(2)已知集合C={x|a+1<x<2a-1},若A∩C=C,求实数a的取值范围.
分析 (1)求解指数不等式和对数不等式化简集合A,B,然后直接利用交集补集并集运算求解;
(2)由A∩C=C,结合两集合端点值间的关系得不等式组求解.
解答 解:(1)∵A={x|2≤2x≤16}={x|1≤x≤4}=[1,4],
B={x|log${\;}_{\frac{1}{3}}$x<-1}={x|x>3}=(3,+∞),
∴A∩B=(3,4],
∴∁RB=(-∞,3],
∴∁RB∪A=(-∞,4],
(2)∵A∩C=C,
∴C⊆A,
当C=∅时,由a+1≥2a-1,解的a≤2,
当C≠∅时,由1≤a+1<2a-1≤4,解的2≤a≤$\frac{5}{2}$,
综上所述a的取值范围为(-∞,$\frac{5}{2}$].
点评 本题考查了交、并、补集的混合运算,考查了指数不等式和对数不等式的解法,是基础题.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
9.若函数f(x)是定义在R上的偶函数,在(-∞,0]上是减函数,且f(2)=0,则使得(x-2)f(x)<0的x的取值范围是( )
| A. | (-∞,-2) | B. | (2,+∞) | C. | (-∞,-2)∪(2,+∞) | D. | (-2,2) |
16.设定义在R上的函数f(x)=$\left\{\begin{array}{l}{2(x=0)}\\{lo{g}_{3}|x|(x≠0)}\end{array}\right.$,若关于x的方程f2(x)+bf(x)+c=0恰有3个不同的实数解,则bc=( )
| A. | -9 | B. | 9 | C. | -16 | D. | 16 |
6.在△ABC中,角A,B,C的对边分别为a,b,c,若a=1,b=$\sqrt{2}$,B=45°,则角A=( )
| A. | 30° | B. | 60° | C. | 30°或150° | D. | 60°或120° |
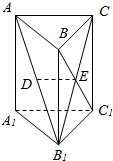 如图:在三棱柱ABC-A1B1C1中,已知AA1⊥底面ABC,AC⊥BC.四边形BB1C1C为正方形,设AB1的中点为D,B1C∩BC1=E.求证
如图:在三棱柱ABC-A1B1C1中,已知AA1⊥底面ABC,AC⊥BC.四边形BB1C1C为正方形,设AB1的中点为D,B1C∩BC1=E.求证 如图,在四棱锥P-ABCD中,AB∥CD,AC⊥BD,AC与BD交于点O,且平面PAC⊥底面ABCD,E为棱PA上一点.
如图,在四棱锥P-ABCD中,AB∥CD,AC⊥BD,AC与BD交于点O,且平面PAC⊥底面ABCD,E为棱PA上一点.